Panel Regression Analysis

MP223 - Applied Econometrics Methods for the Social Sciences

Eduard Bukin

R setup

library(tidyverse)       # for data wrangling
library(alr4)            # for the data sets #
library(GGally)
library(parameters)
library(performance)
library(see)
library(car)
library(broom)
library(modelsummary)
library(texreg)
library(insight)
library(scales)
library(glue)

ggplot2::theme_set(ggplot2::theme_bw())

knitr::opts_chunk$set(
  fig.width = 10,
  fig.asp = 0.618,
  fig.retina = 3,
  dpi = 300,
  out.width = "100%", 
  message = FALSE,
  echo = TRUE, 
  cache = TRUE
)

# Custom functions to summaries data nicely
get_signif <- 
  function(x) {
    symnum(
      x,
      corr = FALSE,
      na = FALSE,
      cutpoints = c(0, 0.001, 0.01, 0.05, 0.1, 1),
      symbols = c("***", "**", "*", ".", " ")
    ) %>% 
      as.character()
  }

tidy_skim <- 
  function(dta) {
    dta %>%
      select(- any_of(c("id", "time"))) %>% 
      skimr::skim_without_charts() %>%
      as_tibble() %>%
      select(any_of(c("skim_variable","n_missing")), contains("numeric")) %>%
      rename_with( ~ str_remove(., "numeric\\."))
  }

tidy_coeftest <- 
  function(
    mod, 
    mod_name = deparse(substitute(mod)), 
    mod_vcov = vcov(mod),
    dig = 3, 
    ...) {
    mod_name_sym <- sym(mod_name)
    mod %>%
      lmtest::coeftest(vcov. = mod_vcov)  %>%
      broom::tidy() %>%
      mutate(
          across(c(estimate, std.error),
                 ~ scales::number(., 1 / 10 ^ dig, big.mark = ",")),
        across(c(p.value), ~ insight::format_p(., stars_only = TRUE)),
        mod_stat := glue::glue("{estimate}{p.value} ({std.error})")
      ) %>%
      select(parameter = term, !!mod_name_sym := mod_stat)
  }

tidy_gof <- 
  function(
    mod, 
    mod_name = deparse(substitute(mod)), 
    dig = 3, 
    ...) {
    mod_sum <- summary(mod)
    mod_sum <- mod_sum$fstatistic
    if (is.vector(mod_sum)) {
      df1 <- mod_sum[[2]]
      df2 <- mod_sum[[3]]
      df <- str_c(c(df1, df2), collapse = "; ")
    } else {
      df <- str_c(mod_sum$parameter, collapse = "; ")
    }
    mod %>%
      broom::glance() %>%
      {
        dta <- .
        if (!"logLik" %in% names(dta)) {
          dta <-
            mutate(dta, logLik = mod %>% stats::logLik() %>% as.numeric())
        }
        
        if (!"AIC" %in% names(dta)) {
          dta <- mutate(dta, AIC = mod %>% stats::AIC() %>% as.numeric())
        }
        
        if (!"BIC" %in% names(dta)) {
          dta <- mutate(dta, BIC = mod %>% stats::BIC() %>% as.numeric())
        }
        dta
      } %>%
      mutate(
        across(any_of(c("r.squared", "deviance", "adj.r.squared")), 
               ~ scales::number(., 1 / 10 ^ dig, big.mark = ",")),
        across(any_of(c("statistic", "logLik", "AIC", "BIC")),
               ~ scales::number(., 1, big.mark = ",")),
        `F Statistics (df)` =
          glue("{statistic}{get_signif(p.value)} ", "({df})"),
        nobs = scales::number(nobs, 1, big.mark = ",")
      ) %>%
      select(
        N = nobs,
        `R-sq. adj.` = adj.r.squared,
        `Log likelihood` = logLik,
        AIC,
        BIC,
        `F Statistics (df)`
      ) %>%
      pivot_longer(everything(), 
                   names_to = "parameter", 
                   values_to = mod_name)
  }


tidy_summary <-
  function(mod,
           mod_name = deparse(substitute(mod)),
           mod_vcov = vcov(mod),
           dig = 3,
           ...) {
    
    tidy_coeftest(mod,mod_name = mod_name, mod_vcov = mod_vcov, dig = dig) %>% 
      bind_rows(tidy_gof(mod, mod_name = mod_name, dig = dig))
  }


tidy_summary_list <-
  function(mod_list,
           mod_vcov = NULL,
           dig = 3,
           ...) {
    # browser()
    mod_list %>%
      list(., names(.), seq_along(.)) %>% 
      pmap(~ {
        vcov_here <- vcov(..1)
        if (!is.null(mod_vcov[[..3]]))
          vcov_here <- mod_vcov[[..3]]
        tidy_summary(
          mod = .x,
          mod_name = .y,
          mod_vcov = vcov_here,
          dig = dig
        )
      }) %>%
      reduce(full_join, by = "parameter")
  }

Recap

Ceteris paribus!?
- Why multiple regression is “good”?
- What variables are important when establishing a causal effect of a treatment (key variable)?
- What if we do not have an important variable?
Selection bias = OVB! In multiple regression analysis.
- What does OVB to our regression estimates?
- Bias (inconsistency) of estimates!

Data Types

Cross-sectional data

ID	Y	X1	X2
\(1\)	\(y_{1}\)	\(x^{1}_{1}\)	\(x^{2}_{1}\)
\(2\)	\(y_{2}\)	\(x^{1}_{2}\)	\(x^{2}_{2}\)
\(3\)	\(y_{3}\)	\(x^{1}_{3}\)	\(x^{2}_{3}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(N\)	\(y_{N}\)	\(x^{1}_{N}\)	\(x^{1}_{N}\)

Could be repeated multiple times, but in every repetition, there are different individuals.

Panel data

table with data, where
each individual (cohort) is represented by multiple observations from different time periods.
sometimes, nested cohorts are possible too (region, individual, time).

Panel data

ID	Time	Y	X1	X2
\(1\)	\(1\)	\(y_{11}\)	\(x^{1}_{11}\)	\(x^{2}_{11}\)
\(1\)	\(2\)	\(y_{12}\)	\(x^{1}_{12}\)	\(x^{2}_{12}\)
\(1\)	\(3\)	\(y_{13}\)	\(x^{1}_{13}\)	\(x^{2}_{13}\)
\(2\)	\(2\)	\(y_{22}\)	\(x^{1}_{22}\)	\(x^{2}_{22}\)
\(2\)	\(3\)	\(y_{23}\)	\(x^{1}_{23}\)	\(x^{2}_{23}\)
\(3\)	\(1\)	\(y_{31}\)	\(x^{1}_{31}\)	\(x^{2}_{31}\)
\(3\)	\(2\)	\(y_{32}\)	\(x^{1}_{32}\)	\(x^{2}_{32}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(N\)	\(1\)	\(y_{N1}\)	\(x^{1}_{N1}\)	\(x^{1}_{N1}\)
\(N\)	\(2\)	\(y_{N2}\)	\(x^{1}_{N2}\)	\(x^{2}_{N2}\)

Panel data: Balanced and Unbalanced

Balanced				Unbalanced
\(\text{ID}\)	\(\text{Time}\)	\(Y\)	\(X\)	\(\text{ID}\)	\(\text{Time}\)	\(Y\)	\(X\)
1	1	\(Y_{11}\)	\(X_{11}\)	1	1	\(Y_{11}\)	\(X_{11}\)
1	2	\(Y_{12}\)	\(X_{12}\)	1	2	\(Y_{12}\)	\(X_{12}\)
1	3	\(Y_{13}\)	\(X_{13}\)	2	2	\(Y_{22}\)	\(X_{22}\)
2	1	\(Y_{21}\)	\(X_{21}\)	2	3	\(Y_{23}\)	\(X_{23}\)
2	2	\(Y_{22}\)	\(X_{22}\)	3	3	\(Y_{33}\)	\(X_{33}\)
2	3	\(Y_{23}\)	\(X_{23}\)	4	1	\(Y_{31}\)	\(X_{31}\)

Using Panel Data …

Important

is a strategy to control unobserved/omitted but fixed effects using time or cohort (individual) dimensions.

Motivation for panel data regression analysis

Example 1: Effect of an employee’s union membership on wage

Does the collective bargaining (union membership) has any effect on wages?

See the following seminal papers: (Freeman 1984; Card 1996)

\[log(\text{Wage}_{it}) = \beta_0 + \beta_1 \cdot \text{Union}_{it} + \beta_2 \cdot {X_{it}} + \beta_3 \cdot \text{Ability}_{i} + \epsilon_{it}\]

where \(i\) is the individual and \(t\) is the time dimension;

Is there an endogeneity problem?

Is there a source of endogeneity / selection bias here?
- Any ideas?
- Any ideas….
Ability:
- not observable ;
- time invariant;
- correlates with \(X\) and \(Y\);
Omitting ability causes the OVB!

Solution: use the panel data

Most of the individual-related characteristics change over time: wage. union membership, skills, experience.
- These variables will be different each time we record measurements for each individual.
Ability are time-invariant and specific to each individual;
- If we introduce dummy variables for each individual,
- we can approximate different ability levels!

Cross-sectional data and individual dummies

Can we introduce dummy variables for each individual in a cross-section?
- Any ideas?
- Why?….
NO…
- Because the number of independent variables have to be less or equal to the number of observations.

Cross-sectional example

ID	Y	X1	X2	\({ID}_1\)	\({ID}_2\)	\({ID}_3\)	\({ID}_N\)
\(1\)	\(y_{1}\)	\(x^{1}_{1}\)	\(x^{2}_{1}\)	1	0	0	0
\(2\)	\(y_{2}\)	\(x^{1}_{2}\)	\(x^{2}_{2}\)	0	1	0	0
\(3\)	\(y_{3}\)	\(x^{1}_{3}\)	\(x^{2}_{3}\)	0	0	1	0
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(N\)	\(y_{N}\)	\(x^{1}_{N}\)	\(x^{1}_{N}\)	0	0	0	1

Panel data data and individual dummies

ID	Time	Y	X1	X2	\({ID}_1\)	\({ID}_2\)	\({ID}_N\)
\(1\)	\(1\)	\(y_{11}\)	\(x^{1}_{11}\)	\(x^{2}_{11}\)	1	0	0
\(1\)	\(2\)	\(y_{12}\)	\(x^{1}_{12}\)	\(x^{2}_{12}\)	1	0	0
\(1\)	\(3\)	\(y_{13}\)	\(x^{1}_{13}\)	\(x^{2}_{13}\)	1	0	0
\(2\)	\(2\)	\(y_{22}\)	\(x^{1}_{22}\)	\(x^{2}_{22}\)	0	1	0
\(2\)	\(3\)	\(y_{23}\)	\(x^{1}_{23}\)	\(x^{2}_{23}\)	0	1	0
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(N\)	\(1\)	\(y_{N1}\)	\(x^{1}_{N1}\)	\(x^{1}_{N1}\)	0	0	1
\(N\)	\(2\)	\(y_{N2}\)	\(x^{1}_{N2}\)	\(x^{2}_{N2}\)	0	0	1

With the panel data it will work, but…

May be difficult… Any ideas why?…

Number of dummy variables is equal to the number of individuals.
- If we have 5,000 individuals, we have 5,000 regression coefficients.
- What if we have 100,000 individuals?
Having too many regressors remains unbiased, but complicates inference:
- number of degrees of freedom increases;
- adjusted \(R^2\) may shrink to zero;

Panel regression: brief theory

Readings

Key readings:

Mundlak (1961)
Angrist and Pischke (2009) Ch. 5
J. M. Wooldridge (2010);
M. J. Wooldridge (2020);
Söderbom, Teal, and Eberhardt (2014), Ch. 9-11

Terminology:

Pooled OLS (regression without any panel structure);
Fixed Effect Models:
- Least-squares dummy variable (Pooled OLS + individual dummies);
- Within-transformation
- First-difference
- Between transformation (look it up in (Croissant and Millo 2018)!)
Random Effect Model

Pooled OLS

Union example, the short model:

. . . \[log(\text{Wage}_{it}) = \beta_0 + \beta_1 \cdot \text{Union}_{it} + \beta_2 \cdot X_{it} + \epsilon_{it}\]

Estimates are biased because we do not observe ability, which are time-invariant (Mundlak 1961).

Least-squares dummy variable approach

Introduce a vector of dummy variables \(\color{Red}{\delta}\)

\[log(\text{Wage}_{it}) = \beta_0 + \beta_1 \cdot \text{Union}_{it} + \beta_2 \cdot X_{it} + \\ \beta_3 \cdot \color{Red}{\delta_{i}} + \epsilon_{it}\]

Estimates and unbiased (consistent) but inefficient.

Within transformation - Key method

\[log(\text{Wage}_{it} - \overline{\text{Wage}_{i}}) = \\ \beta_0 + \beta_1 \cdot (\text{Union}_{it} - \overline{\text{Union}_{i}}) + \\ \beta_2 \cdot (X_{it} - \overline{\text{X}_{i}}) + \beta_3 \cdot (\text{Ability}_{i} - \overline{\text{Ability}_{i}}) + \\ (\epsilon_{it} - \overline{\epsilon_{i}})\]

Any time-invariant effect will disappear from the regression because: \(\text{Ability}_{i} - \overline{\text{Ability}_{i}} = 0\)
Estimates are identical to the least-squares dummy variable, but SE are more efficient;

ID	Time	\(Y\)	\(Y-\overline{Y}\)	\(X1\)	\(X1-\overline{X1}\)
\(1\)	\(1\)	\(y_{11}\)	\(y_{11} - \overline{y_1}\)	\(x^{1}_{11}\)	\(x^1_{11} - \overline{x^1_1}\)
\(1\)	\(2\)	\(y_{12}\)	\(y_{12} - \overline{y_1}\)	\(x^{1}_{12}\)	\(x^1_{12} - \overline{x^1_1}\)
\(1\)	\(3\)	\(y_{13}\)	\(y_{13} - \overline{y_1}\)	\(x^{1}_{13}\)	\(x^1_{13} - \overline{x^1_1}\)
\(2\)	\(2\)	\(y_{22}\)	\(y_{22} - \overline{y_2}\)	\(x^{1}_{22}\)	\(x^1_{22} - \overline{x^1_2}\)
\(2\)	\(3\)	\(y_{23}\)	\(y_{23} - \overline{y_2}\)	\(x^{1}_{23}\)	\(x^1_{23} - \overline{x^1_2}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(N\)	\(1\)	\(y_{N1}\)	\(y_{N1} - \overline{y_N}\)	\(x^{1}_{N1}\)	\(x^1_{N1} - \overline{x^1_N}\)
\(N\)	\(2\)	\(y_{N2}\)	\(y_{N2} - \overline{y_N}\)	\(x^{1}_{N2}\)	\(x^1_{N2} - \overline{x^1_N}\)

First Difference transformation

\[log(\text{Wage}_{it} - {\text{Wage}_{i,t-1}}) = \\ \beta_0 + \beta_1 \cdot (\text{Union}_{it} - {\text{Union}_{it-1}}) + \\ \beta_2 \cdot (X_{it} - {{X}_{i,t-1}}) + \\ \beta_3 \cdot (\text{Ability}_{i} - {\text{Ability}_{i,t-1}}) + (\epsilon_{it} - {\epsilon_{i,t-1}})\]

Has similar effect as the within transformation.
Sacrifices at least one time dimension.
Relaxes autocorrelation assumption.
May be not possible with unbalanced data.

Fixed effect model assumptions

Very Important:

NOT ZERO CORRELATION between effects and regressors: \(Cov(\delta_{i},{X}_{it}) \neq 0\)
Strict exogeneity: \(E[\epsilon_{is}| {X}_{it}, \delta_{i}] = 0\)
- \(Cov(\epsilon_{is}, {X}_{jt}) = 0\) and \(Cov(\epsilon_{it}, {X}_{it}) = 0\) , where \(j\neq i\) and \(s\neq t\) ;
- Residuals (\(\epsilon\)) do not correlate with all explanatory variable (\(X\)) in all time periods (\(t\)) and for all individuals (\(i\)).
  - No autocorrelation/serial correlation: \(Cov(\epsilon_{it}, {X}_{i,t-1}) = 0\);
  - No cross-sectional dependence: \(Cov(\epsilon_{it}, {X}_{j,t}) = 0\) (when individual observations react similarly to the common shocks or correlate in space);

Not less important:

Linearity
Homoscedasticity of error terms: \(Var(\delta_{i}|{X}_{it}) = \sigma^2_{\delta}\)

Fixed effect: literature

Seminal papers: Mundlak (1961)
Climate and agriculture: Mendelsohn, Nordhaus, and Shaw (1994), Blanc and Schlenker (2017), Bozzola et al. (2017)
Choice of irrigation: Kurukulasuriya, Kala, and Mendelsohn (2011), Chatzopoulos and Lippert (2015)
Crop choice: Kurukulasuriya et al. (2008), Seo and Mendelsohn (2008a),
Livestock choice Seo et al. (2008), Seo and Mendelsohn (2008b)
Cross-sectional dependence: Conley (1999)

Random Effect Model

Introduce a random component of the error term \(\color{Red}{v}\)

\[log(\text{Wage}_{it}) = \beta_0 + \beta_1 \cdot \text{Union}_{it} + \beta_2 \cdot X_{it} + \beta_3 \cdot \color{Red}{v_{i}} + \epsilon_{it}\]

Difference from the fixed effect model:
- Assumes NO CORRELATION (ZERO CORRELATION) between effects and regressors: \(Cov(v_{i},{X}_{it}) = 0\).
- Ignoring RE causes no bias to the estimates;

Limitations of Fixed and Random effect models

NOT the ultimate solution to Endogeneity.
There might still be some OVB even with the fixed effects.
- Instrumental Variables are possible within the panel regression context too.
Measurement error may cause endogeneity;

Example 1. Unions premium: implication of the Fixed effect model:

Panel regression: Empirical motivation

Example 2. Macro-level data analysis

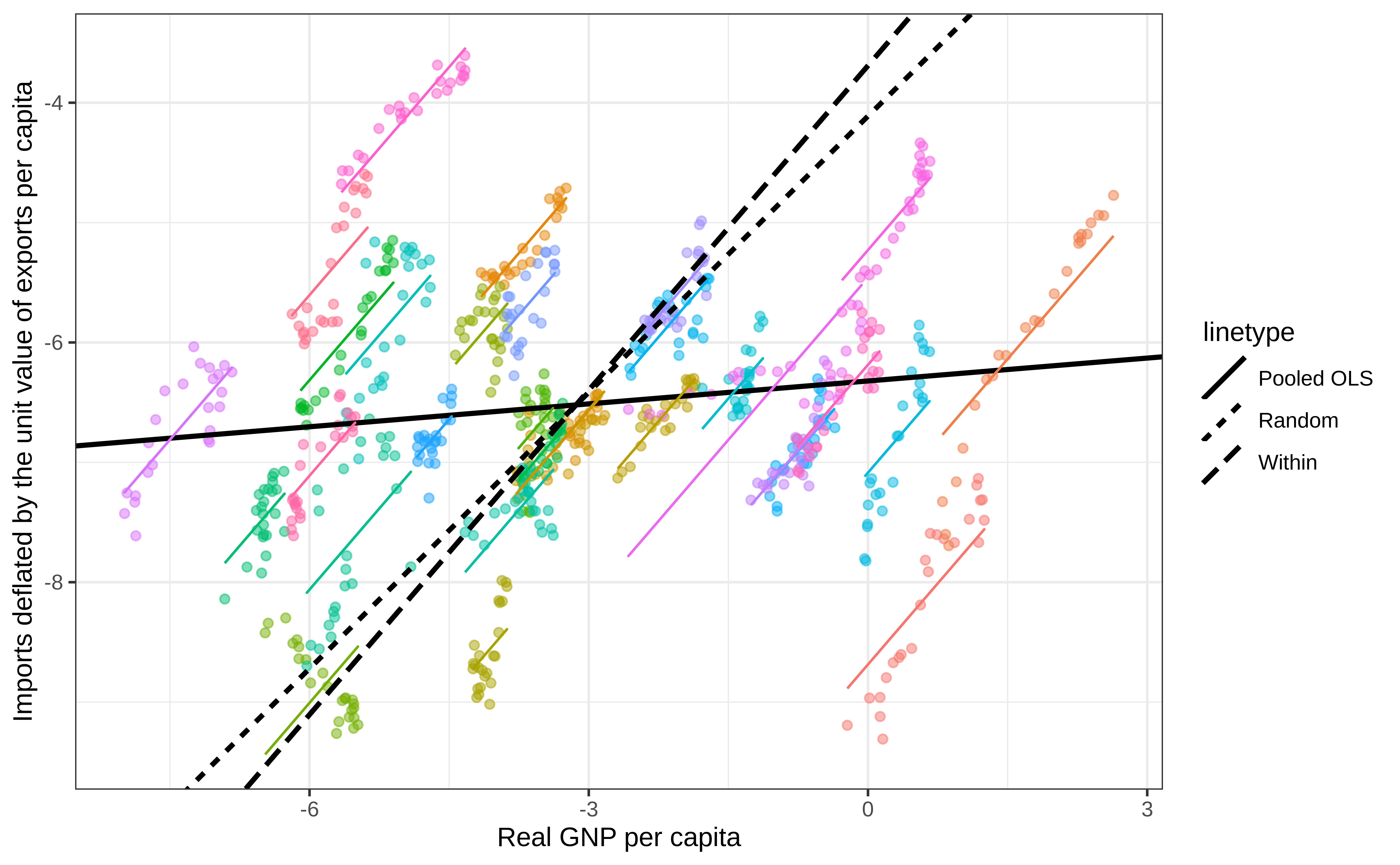
Let us analyze a link between imports and national product based on (Kinal and Lahiri 1993).
Both variables are in per capita and in log.

library(plm); library(pder); library(splm)
data("ForeignTrade", package = "pder")
ForeignTrade <- ForeignTrade %>% 
  select(country, year, exports, imports, gnp) %>% 
  pdata.frame(index = c("country", "year"))
pdim(ForeignTrade)

Balanced Panel: n = 31, T = 24, N = 744

head(ForeignTrade)

                 country year  exports  imports      gnp
Indonesia-1963 Indonesia 1963 -7.62723 -9.19358 -0.22242
Indonesia-1964 Indonesia 1964 -7.61279 -8.96084  0.12960
Indonesia-1965 Indonesia 1965 -7.65318 -8.96664  0.01653
Indonesia-1966 Indonesia 1966 -7.67038 -9.30862  0.15908
Indonesia-1967 Indonesia 1967 -7.67121 -9.12042  0.13064
Indonesia-1968 Indonesia 1968 -7.42591 -8.79655  0.19652

Relationship between GNP and imports

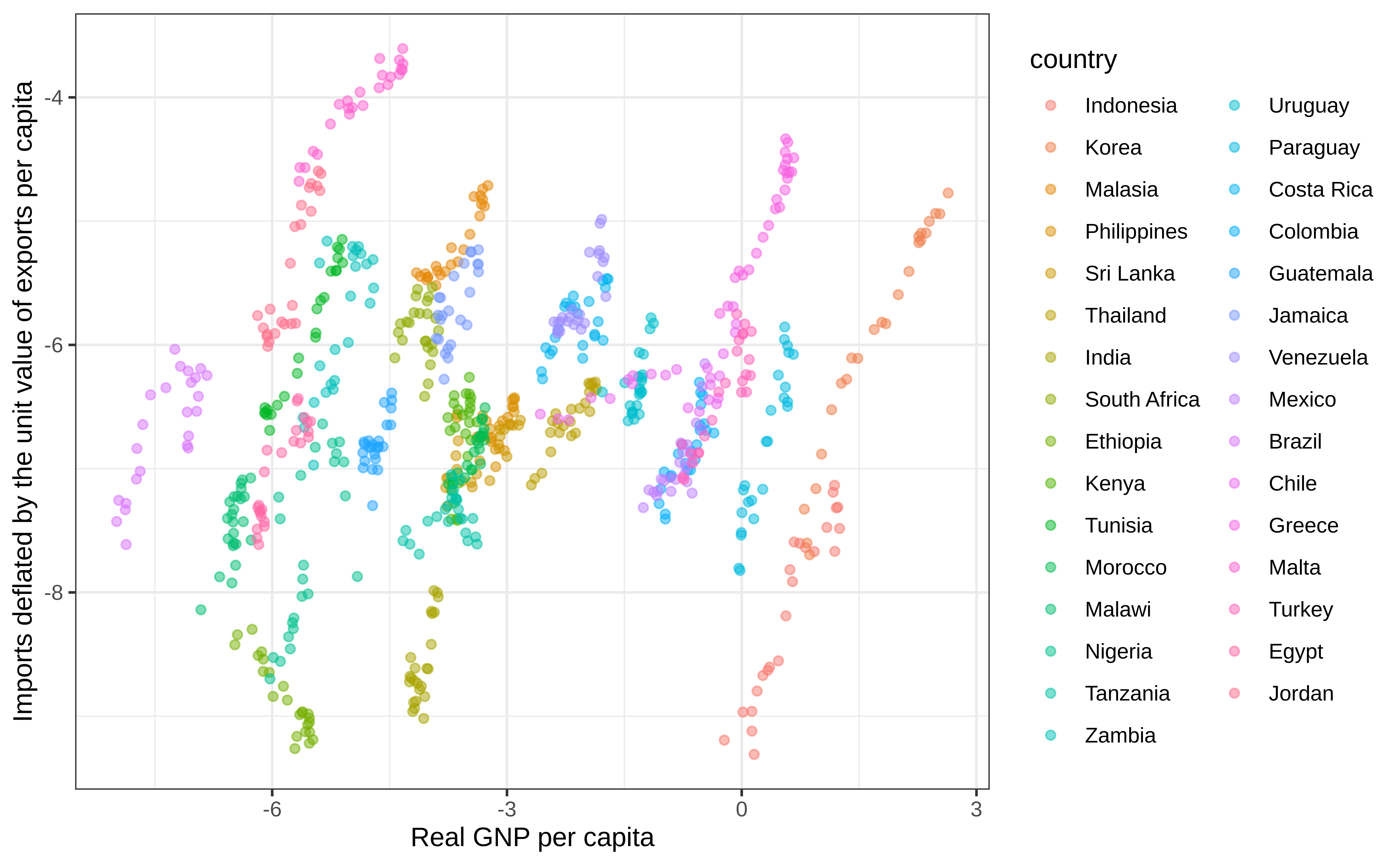
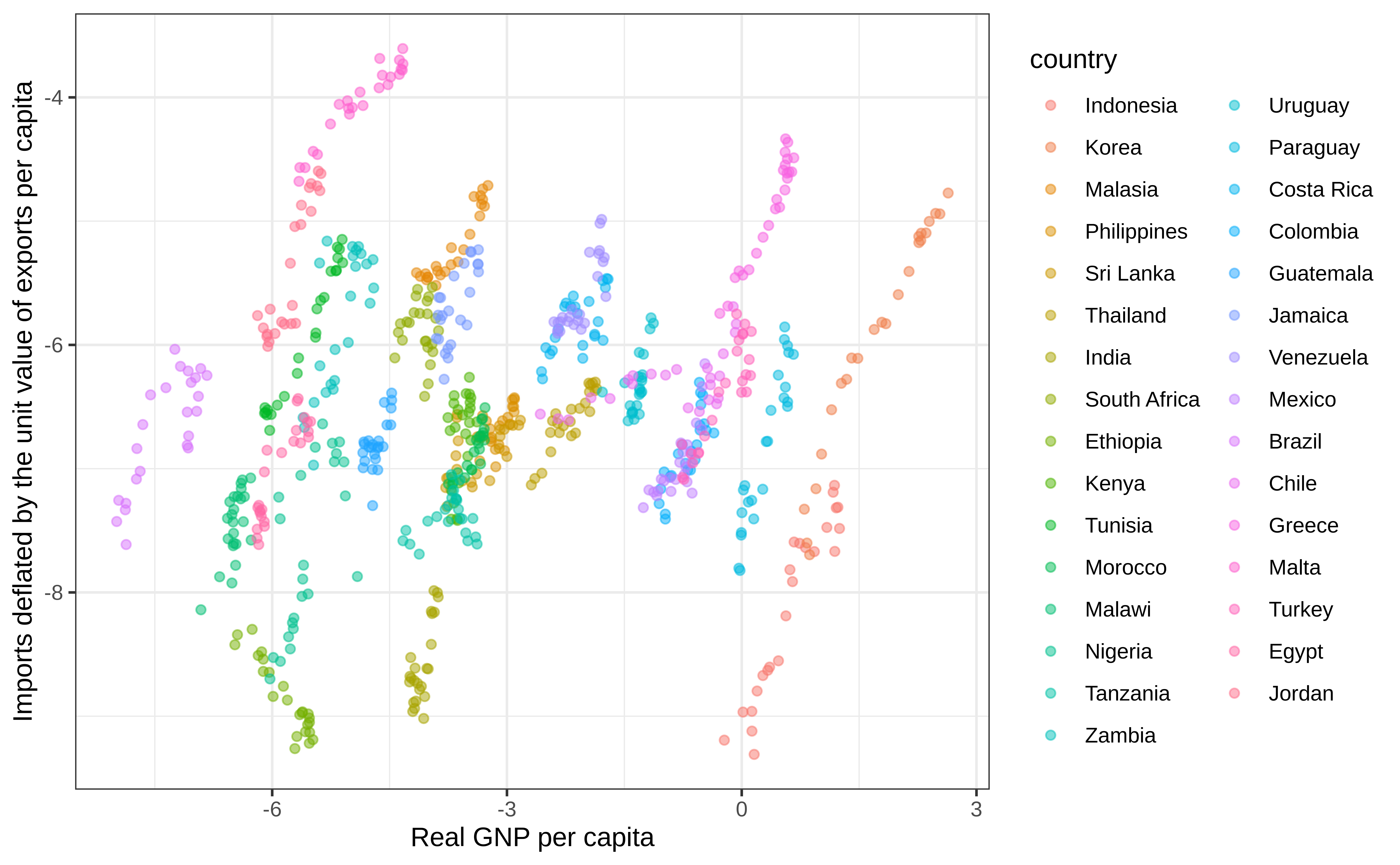
Pooled

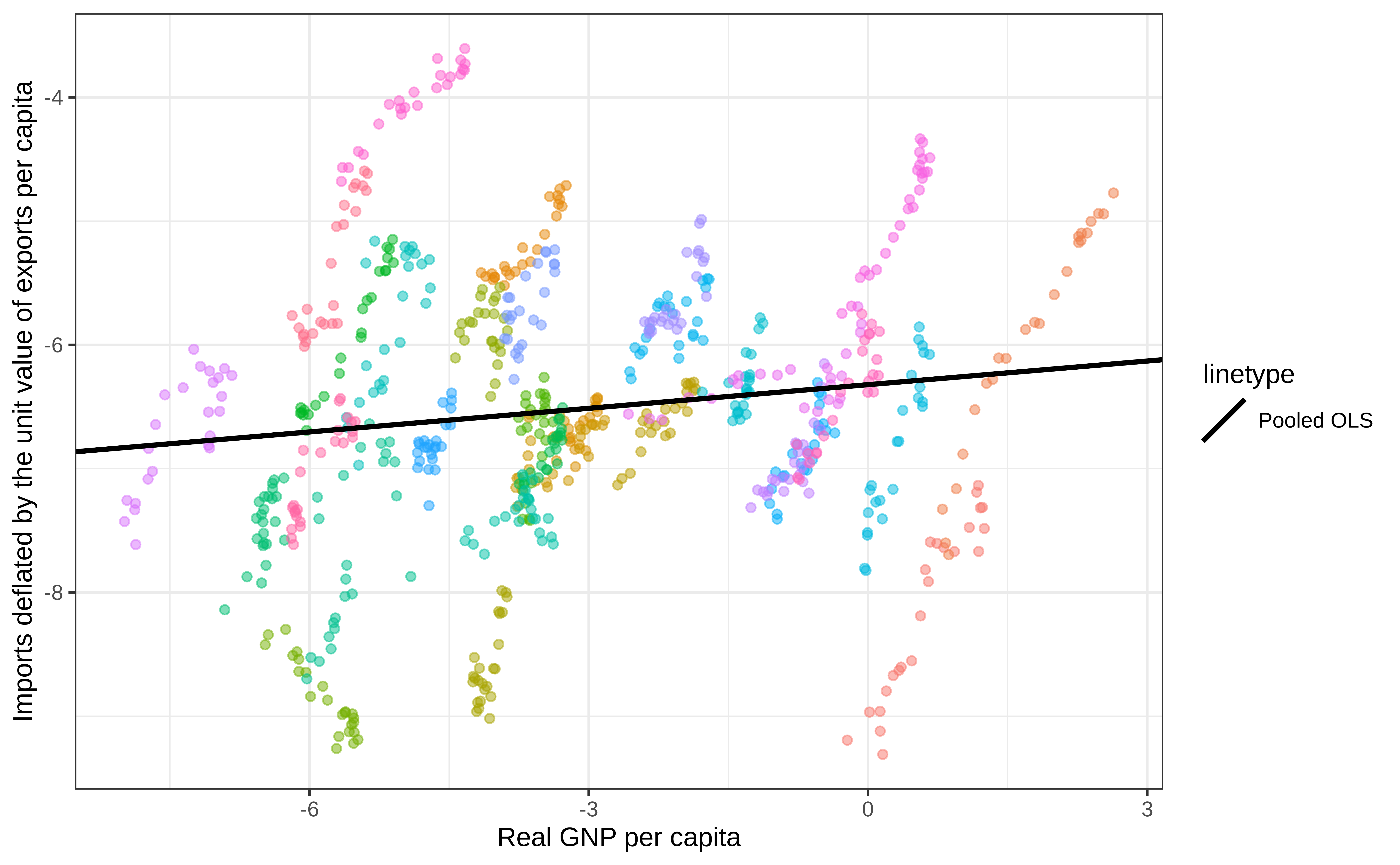
Pooled + Within

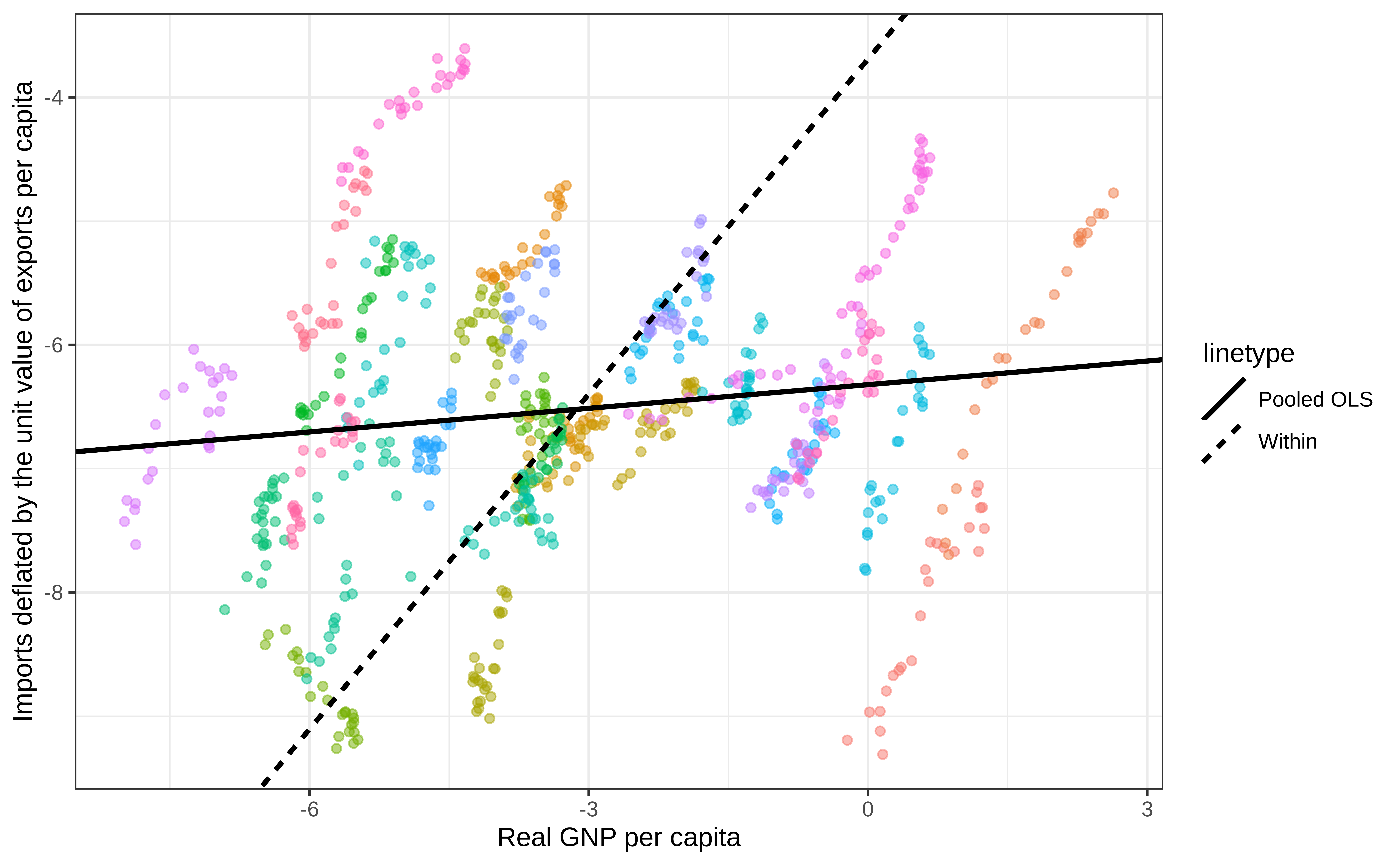
Pooled + Within + Random

Panel regression: Empirical practice

General algorithm

Pooled OLS using;
- Gauss-Markov assumption validation: Linearity, Collinearity, No endogeneity, Homoscedasticity, validation;
FE: Fixed Effect. Within-transformation. Individual, Time or Two-ways effects;
- F-test and LM test on FE consistency against pooled;
RE: Random Effect;
- Hausman test, Chamberlain test, Angrist and Newey on effects’ correlation with regressors of RE consistency against the FE;
Choosing the appropriate functional form;
Serial correlation and cross-sectional dependence tests;
Robust standard errors:
- Clustered SE and/or heteroscedasticity and/or autocorrelation robust SE;
Summary and interpretation;

Example 3. Micro-level application `RiceFarms`

Let us explore the determinants of rice farms productivity.

Tip

We want to understand if larger farms are more productive compared to smaller once.

Farm-specific Rice production function (1)

We employ a production function approach, relying on the Cobb-Douglas Production function:

\[\ln y = \ln \beta_0 + \sum_{n = 1}^{N} \beta_n \ln x_n + \sum_{k = 1}^{K} \gamma_k \delta_k + \epsilon\]

where,

\(y\) is the output and \(x_n\) are the inputs all in physical mass (or monetary value); \(N\) is the number of independent variables;
\(\delta_k\) are the shift parameters of additional dummy variables;
\(\beta_0\) , \(\beta_n\) , \(\gamma_n\) are the estimated coefficients;

Farm-specific Rice production function (2)

Inputs are: land, seeds, urea, pesticide and labor;
Output: rice production in physical mass;
short model (all things are in log): . . .

\[\text{output} = A_0 + \beta_1 \cdot \text{land} + \beta_2 \cdot \text{labor} + \\ \beta_3 \cdot \text{seed} + \beta_4 \cdot \text{urea} + \beta_1 \cdot \text{pesticide}\]

What are the ex-ante expectations about the regression coefficients?
- Ideas? …

What about OVB? (3)

What omitted variables could cause bias of the regression?
- Any!? …
- Any!? …
- Capital, Ability, Climate, Geography…
Let us speculate on the bias of land estimated given exclusion of ability.
- Long model.
- Short model.
- OVB formula.
Educated guess about bias of the estimates.

Farm-level data

Following data RiceFarms is used from package splm. We only use a subset of variables:
- output - gross output of rice in kg
- land - the total area cultivated with rice, measured in hectares
- seed - seed in kilogram
- urea - urea in kilogram
- pesticide - urea in kilogram
- labor - total labor (excluding harvest labor)
We calculate logs of all variables.
we do not use logs for summary statistics.

Data glimpse (1)

data("RiceFarms", package = "splm")
rice_dta_selection <- RiceFarms %>% as_tibble() %>%
  select(
    id, time,
    output = goutput,
    land = size,
    labor = totlabor,
    seed, urea,
    pest = pesticide
  )

rice_dta_1 <- rice_dta_selection %>%
  mutate(across(c(output, land, seed, urea, pest, labor), ~ log(.)))

# Making panel structure
rice_dta_p1 <- rice_dta_1 %>% pdata.frame(index = c("id", "time"))
pdim(rice_dta_p1)

Balanced Panel: n = 171, T = 6, N = 1026

Data glimpse (2)

glimpse(rice_dta_1)

Rows: 1,026
Columns: 8
$ id     <int> 101001, 101001, 101001, 101001, 101001, 101001, 101017, 101017,…
$ time   <dbl> 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, …
$ output <dbl> 8.984694, 8.314587, 7.882315, 8.411833, 9.698920, 9.765604, 8.2…
$ land   <dbl> 1.0986123, 0.6931472, 0.0000000, 0.6931472, 1.2731257, 1.273125…
$ labor  <dbl> 7.977625, 7.675546, 6.980076, 7.645398, 8.265907, 8.165932, 6.6…
$ seed   <dbl> 4.499810, 3.688879, 4.605170, 4.094345, 4.653960, 4.653960, 3.9…
$ urea   <dbl> 6.802395, 6.396930, 6.551080, 6.396930, 5.991465, 5.991465, 4.7…
$ pest   <dbl> 8.699515, 8.006368, 8.517193, 8.517193, 9.230143, 9.230143, -In…

tidy_skim(rice_dta_1)

# A tibble: 6 × 9
  skim_variable n_missing    mean      sd      p0     p25     p50    p75  p100
  <chr>             <int>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>  <dbl> <dbl>
1 output                0    6.73   0.995    3.74    6.04    6.79  7.38   9.95
2 land                  0   -1.30   0.951   -4.61   -1.94   -1.25 -0.693  1.67
3 labor                 0    5.56   0.847    2.83    4.97    5.53  6.08   8.47
4 seed                  0    2.37   0.937    0       1.61    2.30  3.00   7.13
5 urea                  0    3.98   1.16     0       3.22    4.09  4.61   7.13
6 pest                  0 -Inf    NaN     -Inf    -Inf    -Inf     5.58  11.0

Any problems with data?

Any problems with data? (1)

Any? …
pest, when transformed with logs, produces -Inf values.
- Why is that so?
- Any? …
- Because there are zero values of pesticides application \(\ln 0 = - \infty\).

`-Infinity` in logs: lazy solution

Before log transformation, substitute any zero with a small value, for example 0.0001;

rice_dta_lazy <- 
  rice_dta_selection %>% 
  mutate(pest = ifelse(pest <= 0, 0.0001, pest))%>%
  mutate(across(c(output, land, seed, urea, pest, labor), ~ log(.)))
rice_dta_p_lazy <- rice_dta_lazy %>% pdata.frame(index = c("id", "time"))
rice_dta_lazy %>% tidy_skim()

# A tibble: 6 × 9
  skim_variable n_missing  mean    sd    p0   p25   p50    p75  p100
  <chr>             <int> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>
1 output                0  6.73 0.995  3.74  6.04  6.79  7.38   9.95
2 land                  0 -1.30 0.951 -4.61 -1.94 -1.25 -0.693  1.67
3 labor                 0  5.56 0.847  2.83  4.97  5.53  6.08   8.47
4 seed                  0  2.37 0.937  0     1.61  2.30  3.00   7.13
5 urea                  0  3.98 1.16   0     3.22  4.09  4.61   7.13
6 pest                  0 -4.37 7.35  -9.21 -9.21 -9.21  5.58  11.0

`-Infinity` in logs: smart solution

Introduce reverse dummy variables for each variable with log of zero, see: Battese (1997);
Substitute negative infinity with zero.

rice_dta <- 
  rice_dta_selection %>% 
  mutate(pest_revdum = ifelse(pest <= 0, 1, 0),
    across(c(output, land, seed, urea, pest, labor), ~ log(.)),
    pest = ifelse(is.infinite(pest), 0, pest)) 
rice_dta_p <- rice_dta %>% pdata.frame(index = c("id", "time"))
rice_dta %>% tidy_skim()

# A tibble: 7 × 9
  skim_variable n_missing   mean    sd    p0   p25   p50    p75  p100
  <chr>             <int>  <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>
1 output                0  6.73  0.995  3.74  6.04  6.79  7.38   9.95
2 land                  0 -1.30  0.951 -4.61 -1.94 -1.25 -0.693  1.67
3 labor                 0  5.56  0.847  2.83  4.97  5.53  6.08   8.47
4 seed                  0  2.37  0.937  0     1.61  2.30  3.00   7.13
5 urea                  0  3.98  1.16   0     3.22  4.09  4.61   7.13
6 pest                  0  2.04  3.15   0     0     0     5.58  11.0 
7 pest_revdum           0  0.695 0.461  0     0     1     1      1

Data exploration

library(GGally)
rice_dta %>% select(-id, -time) %>% ggpairs()

Step 1.1 Pooled OLS

rice_pooled <- 
  plm(output ~ land + labor + seed + urea + pest + pest_revdum, 
      rice_dta_p, model = "pooling")
rice_pooled_2 <-   
  lm(output ~ land + labor + seed + urea + pest + pest_revdum, rice_dta_p)
tidy_summary_list(list(pooled_plm = rice_pooled, pooled_lm = rice_pooled_2))

# A tibble: 13 × 3
   parameter         pooled_plm         pooled_lm       
   <chr>             <glue>             <glue>          
 1 (Intercept)       4.314*** (0.219)   4.314*** (0.219)
 2 land              0.435*** (0.030)   0.435*** (0.030)
 3 labor             0.253*** (0.028)   0.253*** (0.028)
 4 seed              0.148*** (0.026)   0.148*** (0.026)
 5 urea              0.171*** (0.016)   0.171*** (0.016)
 6 pest              0.091*** (0.017)   0.091*** (0.017)
 7 pest_revdum       0.513*** (0.117)   0.513*** (0.117)
 8 N                 1,026              1,026           
 9 R-sq. adj.        0.875              0.875           
10 Log likelihood    -379               -379            
11 AIC               775                775             
12 BIC               814                814             
13 F Statistics (df) 1,198*** (6; 1019) 1,198*** (6)

Step 1.2 Linearity and homoscedasticity

check_model(rice_pooled_2, check = c("linearity", "homogeneity"))

Step 2.1 Fixed Effect

rice_fe <- 
  plm(output ~ land + labor + seed + urea + pest + pest_revdum, 
      rice_dta_p, model = "within", effect = "individual")

tidy_summary_list(list(pooled = rice_pooled, FE = rice_fe))

# A tibble: 13 × 3
   parameter         pooled             FE              
   <chr>             <glue>             <glue>          
 1 (Intercept)       4.314*** (0.219)   <NA>            
 2 land              0.435*** (0.030)   0.420*** (0.036)
 3 labor             0.253*** (0.028)   0.271*** (0.033)
 4 seed              0.148*** (0.026)   0.124*** (0.030)
 5 urea              0.171*** (0.016)   0.163*** (0.019)
 6 pest              0.091*** (0.017)   0.110*** (0.020)
 7 pest_revdum       0.513*** (0.117)   0.635*** (0.135)
 8 N                 1,026              1,026           
 9 R-sq. adj.        0.875              0.676           
10 Log likelihood    -379               -245            
11 AIC               775                504             
12 BIC               814                538             
13 F Statistics (df) 1,198*** (6; 1019) 386*** (6; 849)

Step 2.1 lazy versus reverse dummy

Code

rice_fe_lazy <- 
  plm(output ~ land + labor + seed + urea + pest, 
      rice_dta_p_lazy, model = "within", effect = "individual")
rice_pooled_lazy <- 
  plm(output ~ land + labor + seed + urea + pest, 
      rice_dta_p_lazy, model = "pooling")

list(pooled = rice_pooled, `pooled (lazy)` = rice_pooled_lazy, `FE (rev. dumy)` = rice_fe, `FE (lazy)` = rice_fe_lazy) %>% 
  tidy_summary_list()

# A tibble: 13 × 5
   parameter         pooled         `pooled (lazy)` `FE (rev. dumy)` `FE (lazy)`
   <chr>             <glue>         <glue>          <glue>           <glue>     
 1 (Intercept)       4.314*** (0.2… 4.853*** (0.19… <NA>             <NA>       
 2 land              0.435*** (0.0… 0.436*** (0.03… 0.420*** (0.036) 0.421*** (…
 3 labor             0.253*** (0.0… 0.247*** (0.02… 0.271*** (0.033) 0.264*** (…
 4 seed              0.148*** (0.0… 0.164*** (0.02… 0.124*** (0.030) 0.134*** (…
 5 urea              0.171*** (0.0… 0.179*** (0.01… 0.163*** (0.019) 0.174*** (…
 6 pest              0.091*** (0.0… 0.006*** (0.00… 0.110*** (0.020) 0.008*** (…
 7 pest_revdum       0.513*** (0.1… <NA>            0.635*** (0.135) <NA>       
 8 N                 1,026          1,026           1,026            1,026      
 9 R-sq. adj.        0.875          0.872           0.676            0.666      
10 Log likelihood    -379           -391            -245             -261       
11 AIC               761            785             492              525        
12 BIC               766            790             497              529        
13 F Statistics (df) 1,198*** (6; … 1,402*** (5; 1… 386*** (6; 849)  444*** (5;…

Step 2.2 F test for individual effects

Compares FE model to OLS. OLS is always consistent, when Gauss-Markov assumptions are satisfied.
- H0: One model is inconsistent.
- H1: Both models are equally consistent.

pFtest(rice_fe, rice_pooled)


    F test for individual effects

data:  output ~ land + labor + seed + urea + pest + pest_revdum
F = 1.4988, df1 = 170, df2 = 849, p-value = 0.0001704
alternative hypothesis: significant effects

Step 2.3 Lagrange Multiplier Tests

Compares FE model to OLS. OLS is always consistent, when Gauss-Markov assumptions are satisfied.
- H0: One model is inconsistent.
- H1: Both models are equally consistent.

plmtest(rice_pooled, effect = "individual", type = "honda")


    Lagrange Multiplier Test - (Honda) for balanced panels

data:  output ~ land + labor + seed + urea + pest + pest_revdum
normal = 3.7129, p-value = 0.0001025
alternative hypothesis: significant effects

plmtest(rice_pooled, effect = "individual", type = "bp")


    Lagrange Multiplier Test - (Breusch-Pagan) for balanced panels

data:  output ~ land + labor + seed + urea + pest + pest_revdum
chisq = 13.785, df = 1, p-value = 0.0002049
alternative hypothesis: significant effects

Step 3.1 Random Effect

rice_re <- 
  plm(output ~ land + labor + seed + urea + pest + pest_revdum, 
      rice_dta_p, model = "random", effect = "individual")
list(pooled = rice_pooled, FE = rice_fe, RE = rice_re) %>% 
  tidy_summary_list()

# A tibble: 13 × 4
   parameter         pooled             FE               RE              
   <chr>             <glue>             <glue>           <glue>          
 1 (Intercept)       4.314*** (0.219)   <NA>             4.277*** (0.222)
 2 land              0.435*** (0.030)   0.420*** (0.036) 0.434*** (0.031)
 3 labor             0.253*** (0.028)   0.271*** (0.033) 0.258*** (0.029)
 4 seed              0.148*** (0.026)   0.124*** (0.030) 0.143*** (0.027)
 5 urea              0.171*** (0.016)   0.163*** (0.019) 0.169*** (0.016)
 6 pest              0.091*** (0.017)   0.110*** (0.020) 0.097*** (0.018)
 7 pest_revdum       0.513*** (0.117)   0.635*** (0.135) 0.547*** (0.118)
 8 N                 1,026              1,026            1,026           
 9 R-sq. adj.        0.875              0.676            0.853           
10 Log likelihood    -379               -245             -339            
11 AIC               761                492              680             
12 BIC               766                497              685             
13 F Statistics (df) 1,198*** (6; 1019) 386*** (6; 849)  5,967*** (6)

Step 3.2 Hausman Test for Panel Models

Compares RE to FE model. FE is assumed to be consistent
- H0: One model is inconsistent.
- H1: Both models are equally consistent.

phtest(rice_fe, rice_re)


    Hausman Test

data:  output ~ land + labor + seed + urea + pest + pest_revdum
chisq = 7.285, df = 6, p-value = 0.2953
alternative hypothesis: one model is inconsistent

Fixed Effect model is recommended

Step 4.1 Serial correlation and cross-sectional dependence

Wooldridge’s test for unobserved individual effects
- H0: no unobserved effects
- H1: some effects also dues to serial correlation

pwtest(rice_pooled)


    Wooldridge's test for unobserved individual effects

data:  formula
z = 2.1603, p-value = 0.03075
alternative hypothesis: unobserved effect

Step 4.2 lm tests for random effects and/or serial correlation

H0: serial correlation is zero
H1: some serial correlation

pbsytest(rice_pooled, test = "ar")


    Bera, Sosa-Escudero and Yoon locally robust test - balanced panel

data:  formula
chisq = 20.988, df = 1, p-value = 4.622e-06
alternative hypothesis: AR(1) errors sub random effects

pbsytest(rice_pooled, test = "re")


    Bera, Sosa-Escudero and Yoon locally robust test (one-sided) - balanced
    panel

data:  formula
z = 0.38656, p-value = 0.3495
alternative hypothesis: random effects sub AR(1) errors

Step 4.3 Breusch-Godfrey and Durbin-Watson tests

H0: serial correlation is zero
H0: some serial correlation

pbgtest(rice_fe)


    Breusch-Godfrey/Wooldridge test for serial correlation in panel models

data:  output ~ land + labor + seed + urea + pest + pest_revdum
chisq = 312.08, df = 6, p-value < 2.2e-16
alternative hypothesis: serial correlation in idiosyncratic errors

pbgtest(rice_fe, order = 2)


    Breusch-Godfrey/Wooldridge test for serial correlation in panel models

data:  output ~ land + labor + seed + urea + pest + pest_revdum
chisq = 57.029, df = 2, p-value = 4.133e-13
alternative hypothesis: serial correlation in idiosyncratic errors

pdwtest(rice_fe)


    Durbin-Watson test for serial correlation in panel models

data:  output ~ land + labor + seed + urea + pest + pest_revdum
DW = 2.0627, p-value = 0.8511
alternative hypothesis: serial correlation in idiosyncratic errors

Step 5. Robust and clustered standard errors (1)

library(lmtest); library(car); library(sandwich); options(digits = 4, scipen = 15)
# Regular SE
vcov(rice_fe)

                    land       labor        seed        urea         pest
land         0.001307260 -0.00059769 -0.00041874 -0.00014361 -0.000006703
labor       -0.000597690  0.00110633 -0.00024768 -0.00007864  0.000030847
seed        -0.000418745 -0.00024768  0.00093011 -0.00012979 -0.000041049
urea        -0.000143612 -0.00007864 -0.00012979  0.00037163 -0.000047684
pest        -0.000006703  0.00003085 -0.00004105 -0.00004768  0.000383951
pest_revdum -0.000010199  0.00013112 -0.00025183 -0.00023079  0.002579932
            pest_revdum
land         -0.0000102
labor         0.0001311
seed         -0.0002518
urea         -0.0002308
pest          0.0025799
pest_revdum   0.0183242

# Clustered, heteroscedasticity and autocorrelation robust SE
vcovHC(rice_fe, method = "arellano", type = "HC0", cluster = "group")

                  land       labor        seed        urea        pest
land         0.0022017 -0.00090745 -0.00058997 -0.00034714  0.00011641
labor       -0.0009074  0.00117256 -0.00011760  0.00001305 -0.00002128
seed        -0.0005900 -0.00011760  0.00131948 -0.00040185 -0.00001704
urea        -0.0003471  0.00001305 -0.00040185  0.00065293 -0.00009713
pest         0.0001164 -0.00002128 -0.00001704 -0.00009713  0.00033325
pest_revdum  0.0008926 -0.00018949 -0.00015076 -0.00065111  0.00226554
            pest_revdum
land          0.0008926
labor        -0.0001895
seed         -0.0001508
urea         -0.0006511
pest          0.0022655
pest_revdum   0.0162579
attr(,"cluster")
[1] "group"

Step 5. Robust and clustered standard errors (2)

coeftest(rice_fe,
         vcov. = vcovHC(rice_fe, method = "arellano", 
                        type = "HC0", cluster = "group"))


t test of coefficients:

            Estimate Std. Error t value             Pr(>|t|)    
land          0.4198     0.0469    8.95 < 0.0000000000000002 ***
labor         0.2708     0.0342    7.91    0.000000000000008 ***
seed          0.1238     0.0363    3.41              0.00068 ***
urea          0.1629     0.0256    6.38    0.000000000299222 ***
pest          0.1103     0.0183    6.04    0.000000002278921 ***
pest_revdum   0.6350     0.1275    4.98    0.000000770311250 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Step 5. Robust and clustered standard errors (2)

Code

tidy_summary_list( 
  mod_list = 
    list(`FE regular SE` = rice_fe, 
         `FE cl. het. robust` = rice_fe, 
         `FE cl. het. autocor. robust` = rice_fe),
  mod_vcov = list(
    vcov(rice_fe),
    vcovHC(rice_fe, method = "white1", type = "HC0"),
    vcovHC(rice_fe, method = "arellano", type = "sss")
    )
)

# A tibble: 12 × 4
   parameter         `FE regular SE`  `FE cl. het. robust` `FE cl. het. autoco…`
   <chr>             <glue>           <glue>               <glue>               
 1 land              0.420*** (0.036) 0.420*** (0.040)     0.420*** (0.047)     
 2 labor             0.271*** (0.033) 0.271*** (0.032)     0.271*** (0.034)     
 3 seed              0.124*** (0.030) 0.124*** (0.029)     0.124*** (0.037)     
 4 urea              0.163*** (0.019) 0.163*** (0.021)     0.163*** (0.026)     
 5 pest              0.110*** (0.020) 0.110*** (0.017)     0.110*** (0.018)     
 6 pest_revdum       0.635*** (0.135) 0.635*** (0.117)     0.635*** (0.128)     
 7 N                 1,026            1,026                1,026                
 8 R-sq. adj.        0.676            0.676                0.676                
 9 Log likelihood    -245             -245                 -245                 
10 AIC               504              504                  504                  
11 BIC               538              538                  538                  
12 F Statistics (df) 386*** (6; 849)  386*** (6; 849)      386*** (6; 849)

Are larger farms more productive?

Tip

Remember:

We want to understand if larger farms are more productive compared to smaller once.

It is possible to understand by performing a hypothesis testing about a linear combination of parameters taking into consideration their covariance.

Linear hypothesis (1)

lh_1 <- 
  linearHypothesis(rice_fe,
                   "land + labor + seed + urea + pest = 1",
                   vcov. = vcovHC(rice_fe))
lh_1

Linear hypothesis test

Hypothesis:
land  + labor  + seed  + urea  + pest = 1

Model 1: restricted model
Model 2: rice_fe

Note: Coefficient covariance matrix supplied.

  Res.Df Df Chisq Pr(>Chisq)   
1    850                       
2    849  1  8.18     0.0042 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Sum of the linear combinations
attr(lh_1, "value") %>% as.vector()

[1] 0.08768

# SE of the linear combinations
attr(lh_1, "vcov") %>% as.vector()

[1] 0.0009399

Linear hypothesis: delta method (2)

deltaMethod(
  rice_fe, 
  "land + labor + seed + urea + pest",
  vcov. = vcovHC(rice_fe)
)

                                  Estimate     SE  2.5 % 97.5 %
land + labor + seed + urea + pest   1.0877 0.0307 1.0276   1.15

Class/Homework

Reproduce example 3 from the class

Instead of using a Cobb-Douglas production function, use the Translog production function.
Reduce number of regressors to land, labor and seeds for simplicity.
Compute the marginal effects of coefficients.

. . . \[\ln y = \beta_0 + \sum_{n = 1}^{N} \beta_n \ln x_n + \\ \frac{1}{2} \sum_{n = 1}^{N} \sum_{m = 1}^{M} \beta_{nm} \ln x_n \ln x_m + \sum_{k = 1}^{K} \gamma_k \delta_k + \epsilon\]

where,

\(\ln x_n \ln x_m\) are the interaction terms between all combination of two regressors.
Everything else is the same as in Cobb-Douglas.

Take away

Data types: cross-sectional and panel balanced and unbalanced
Why panel data:
FE vs RE;
- Correlated and uncorrelated individual effects
- Limitations of the panel regression methods
- Within, first difference, Random effect
Practical application;
- Fitting panel regression
- Cobb-Douglas and Translog production function
- Model selection routine
- Statistical testing
- Standard Errors correction
- Results presentation
Linear hypothesis testing
- Linear combination of parameters
- Delta method

References

Angrist, Joshua D., and Jörn-Steffen Pischke. 2009. Mostly Harmless Econometrics. Princeton University Press. https://doi.org/10.1515/9781400829828.

Battese, George E. 1997. “A Note on the Estimation of Cobb-Douglas Production Functions When Some Explanatory Variables Have Zero Values.” Journal of Agricultural Economics 48 (1-3): 250–52. https://doi.org/10.1111/j.1477-9552.1997.tb01149.x.

Blanc, Elodie, and Wolfram Schlenker. 2017. “The Use of Panel Models in Assessments of Climate Impacts on Agriculture.” Review of Environmental Economics and Policy 11 (2): 258–79. https://doi.org/10.1093/reep/rex016.

Bozzola, Martina, Emanuele Massetti, Robert Mendelsohn, and Fabian Capitanio. 2017. “A Ricardian Analysis of the Impact of Climate Change on Italian Agriculture.” European Review of Agricultural Economics 45 (1): 57–79. https://doi.org/10.1093/erae/jbx023.

Card, David. 1996. “The Effect of Unions on the Structure of Wages: A Longitudinal Analysis.” Econometrica 64 (4): 957. https://doi.org/10.2307/2171852.

Chatzopoulos, Thomas, and Christian Lippert. 2015. “Endogenous Farm-Type Selection, Endogenous Irrigation, and Spatial Effects in Ricardian Models of Climate Change.” European Review of Agricultural Economics 43 (2): 217–35. https://doi.org/10.1093/erae/jbv014.

Conley, T. G. 1999. “GMM Estimation with Cross Sectional Dependence.” Journal of Econometrics 92 (1): 1–45. https://doi.org/10.1016/s0304-4076(98)00084-0.

Croissant, Yves, and Giovanni Millo. 2018. Panel Data Econometrics with r. John Wiley & Sons.

Freeman, Richard B. 1984. “Longitudinal Analyses of the Effects of Trade Unions.” Journal of Labor Economics 2 (1): 1–26. https://doi.org/10.1086/298021.

Kinal, T., and K. Lahiri. 1993. “On the Estimation of Simultaneous-Equations Error-Components Models with an Application to a Model of Developing Country Foreign Trade.” Journal of Applied Econometrics 8 (1): 81–92. https://doi.org/10.1002/jae.3950080107.

Kurukulasuriya, Pradeep, Namrata Kala, and Robert Mendelsohn. 2011. “Adaptation and Climate Change Impacts: A Structural Ricardian Model of Irrigation and Farm Income in Africa.” Climate Change Economics 2 (02): 149–74.

Kurukulasuriya, Pradeep, Robert Mendelsohn, Pradeep Kurukulasuriya, and Robert Mendelsohn. 2008. “Crop Switching as a Strategy for Adapting to Climate Change.” https://doi.org/10.22004/AG.ECON.56970.

Mendelsohn, Robert, William D Nordhaus, and Daigee Shaw. 1994. “The Impact of Global Warming on Agriculture: A Ricardian Analysis.” The American Economic Review, 753–71.

Mundlak, Yair. 1961. “Empirical Production Function Free of Management Bias.” Journal of Farm Economics 43 (1): 44. https://doi.org/10.2307/1235460.

Seo, S. Niggol, and Robert Mendelsohn. 2008a. “Measuring Impacts and Adaptations to Climate Change: A Structural Ricardian Model of African Livestock Management.” Agricultural Economics 38 (2): 151–65. https://doi.org/10.1111/j.1574-0862.2008.00289.x.

———. 2008b. “An Analysis of Crop Choice: Adapting to Climate Change in South American Farms.” Ecological Economics 67 (1): 109–16. https://doi.org/10.1016/j.ecolecon.2007.12.007.

Seo, S. Niggol, Robert Mendelsohn, S. Niggol Seo, and Robert Mendelsohn. 2008. “Animal Husbandry in Africa: Climate Change Impacts and Adaptations.” https://doi.org/10.22004/AG.ECON.56968.

Söderbom, Måns, Francis Teal, and Markus Eberhardt. 2014. Empirical Development Economics. ROUTLEDGE. https://www.ebook.de/de/product/21466458/mans_soederbom_francis_teal_markus_eberhardt_empirical_development_economics.html.

Wooldridge, Jeffrey M. 2010. Econometric Analysis of Cross Section and Panel Data. MIT press.

Wooldridge, M. Jeffrey. 2020. Introductory Econometrics: A Modern Approach. South-Western. https://www.cengage.uk/shop/isbn/9781337558860.

Panel Regression Analysis

R setup

Recap

Data Types

Cross-sectional data

Panel data

Panel data

Panel data: Balanced and Unbalanced

Using Panel Data …

Motivation for panel data regression analysis

Example 1: Effect of an employee’s union membership on wage

Is there an endogeneity problem?

Solution: use the panel data

Cross-sectional data and individual dummies

Cross-sectional example

Panel data data and individual dummies

With the panel data it will work, but…

Panel regression: brief theory

Readings

Key readings:

Other readings:

Terminology:

Pooled OLS

Least-squares dummy variable approach

Within transformation - Key method

First Difference transformation

Fixed effect model assumptions

Very Important:

Not less important:

Fixed effect: literature

Random Effect Model

Limitations of Fixed and Random effect models

Example 1. Unions premium: implication of the Fixed effect model:

Panel regression: Empirical motivation

Example 2. Macro-level data analysis

Relationship between GNP and imports

Pooled

Pooled

Pooled + Within

Pooled + Within + Random

Panel regression: Empirical practice

General algorithm

Example 3. Micro-level application RiceFarms

Farm-specific Rice production function (1)

Farm-specific Rice production function (2)

What about OVB? (3)

Farm-level data

Data glimpse (1)

Data glimpse (2)

Any problems with data? (1)

-Infinity in logs: lazy solution

-Infinity in logs: smart solution

Data exploration

Step 1.1 Pooled OLS

Step 1.2 Linearity and homoscedasticity

Step 2.1 Fixed Effect

Step 2.1 lazy versus reverse dummy

Step 2.2 F test for individual effects

Step 2.3 Lagrange Multiplier Tests

Step 3.1 Random Effect

Step 3.2 Hausman Test for Panel Models

Step 4.1 Serial correlation and cross-sectional dependence

Step 4.2 lm tests for random effects and/or serial correlation

Step 4.3 Breusch-Godfrey and Durbin-Watson tests

Step 5. Robust and clustered standard errors (1)

Step 5. Robust and clustered standard errors (2)

Step 5. Robust and clustered standard errors (2)

Are larger farms more productive?

Linear hypothesis (1)

Linear hypothesis: delta method (2)

Class/Homework

Reproduce example 3 from the class

Take away

Take away

References

Example 3. Micro-level application `RiceFarms`

`-Infinity` in logs: lazy solution

`-Infinity` in logs: smart solution