Multiple Lnear Regression

MP223 - Applied Econometrics Methods for the Social Sciences

Eduard Bukin

R setup

library(tidyverse)       # for data wrangling
library(alr4)            # for the data sets #
library(GGally)
library(parameters)
library(performance)
library(see)
library(car)
library(broom)
library(modelsummary)
library(texreg)

ggplot2::theme_set(ggplot2::theme_bw())

knitr::opts_chunk$set(
  fig.width = 10,
  fig.asp = 0.618,
  fig.retina = 3,
  dpi = 300,
  out.width = "100%", 
  message = FALSE,
  echo = TRUE, 
  cache = TRUE
)


my_gof <- function(fit_obj, digits = 4) {
  sum_fit <- summary(fit_obj)
  
  stars <- 
    pf(sum_fit$fstatistic[1],
       sum_fit$fstatistic[2], 
       sum_fit$fstatistic[3],
       lower.tail=FALSE) %>% 
    symnum(corr = FALSE, na = FALSE, 
           cutpoints = c(0,  .001,.01,.05,  1),
           symbols   =  c("***","**","*"," ")) %>% 
    as.character()
  
  list(
    # `R^2` = sum_fit$r.squared %>% round(digits),
    # `Adj. R^2` = sum_fit$adj.r.squared %>% round(digits),
    # `Num. obs.` = sum_fit$residuals %>% length(),
    `Num. df` = sum_fit$df[[2]],
    `F statistic` = 
      str_c(sum_fit$fstatistic[1] %>% round(digits), " ", stars)
  )
}

screen_many_regs <-
  function(fit_obj_list, ..., digits = 4, single.row = TRUE) {
    
    if (class(fit_obj_list) == "lm") 
      fit_obj_list <- list(fit_obj_list)
    
    if (length(rlang::dots_list(...)) > 0)  
      fit_obj_list <- fit_obj_list %>% append(rlang::dots_list(...))
    
    # browser()
    fit_obj_list %>%
      screenreg(
        custom.note =
          map2_chr(., seq_along(.), ~ {
            str_c("Model ", .y, " ", as.character(.x$call)[[2]])
          }) %>%
          c("*** p < 0.001; ** p < 0.01; * p < 0.05", .) %>%
          str_c(collapse = "\n") ,
        digits = digits,
        single.row = single.row,
        custom.gof.rows =
          map(., ~my_gof(.x, digits)) %>%
          transpose() %>%
          map(unlist),
        reorder.gof = c(3, 4, 5, 1, 2)
      )
  }

Example 1: UN11 data

Research question

How GDP per capita \(ppgdp\) and degree of Urbanization \(pctUrban\) affects \(fertility\)?

We explore UN11 data from (Weisberg 2005). 199 observations. - Variables are:

-   `fertility` - number of children per woman;
-   `lifeExpF` - Female life expectancy, years;
-   `ppgdp` - Per capita gross domestic product in US dollars;
-   `pctUrban` - Percent of Urban population;
-   `group` - variable with 3 values "oecd", "africa" and "others";

Data loading

Code

library(alr4)           #install.packages("alr4")
library(tidyverse)      #install.packages("tidyverse")
un_dta <- 
  alr4::UN11 %>%
  as_tibble() %>%
  select(-region)
glimpse(un_dta)

Rows: 199
Columns: 5
$ group     <fct> other, other, africa, africa, other, other, other, other, oe…
$ fertility <dbl> 5.968, 1.525, 2.142, 5.135, 2.000, 2.172, 1.735, 1.671, 1.94…
$ ppgdp     <dbl> 499.0, 3677.2, 4473.0, 4321.9, 13750.1, 9162.1, 3030.7, 2285…
$ lifeExpF  <dbl> 49.49, 80.40, 75.00, 53.17, 81.10, 79.89, 77.33, 77.75, 84.2…
$ pctUrban  <dbl> 23, 53, 67, 59, 100, 93, 64, 47, 89, 68, 52, 84, 89, 29, 45,…

Descriptive statistics

Code

un_dta %>% datasummary_skim(output = "data.frame")

            Unique (#) Missing (%)    Mean      SD   Min Median      Max
1 fertility        193           0     2.8     1.3   1.1    2.3      6.9
2     ppgdp        199           0 13012.0 18412.4 114.8 4684.5 105095.4
3  lifeExpF        192           0    72.3    10.1  48.1   75.9     87.1
4  pctUrban         80           0    57.9    23.4  11.0   59.0    100.0

Data visualization

Code

un_dta %>% 
  select(fertility, lifeExpF, pctUrban, ppgdp, group) %>%
  ggpairs(aes(alpha = 0.6))

Regression

Code

fit1 <- lm(fertility ~ ppgdp + pctUrban , un_dta)
fit1


Call:
lm(formula = fertility ~ ppgdp + pctUrban, data = un_dta)

Coefficients:
(Intercept)        ppgdp     pctUrban  
  4.374e+00   -1.305e-05   -2.491e-02

Reg. summary `base` R

summary(fit1)


Call:
lm(formula = fertility ~ ppgdp + pctUrban, data = un_dta)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.19513 -0.81326 -0.09851  0.61527  2.97892 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.374e+00  2.244e-01  19.489  < 2e-16 ***
ppgdp       -1.304e-05  5.366e-06  -2.431    0.016 *  
pctUrban    -2.491e-02  4.217e-03  -5.907 1.51e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.114 on 196 degrees of freedom
Multiple R-squared:  0.3155,    Adjusted R-squared:  0.3085 
F-statistic: 45.16 on 2 and 196 DF,  p-value: < 2.2e-16

Reg. summary; Coef. `parameters::parameters()`

See: easystats/parameters

library(parameters)
parameters(fit1)

Parameter   | Coefficient |       SE |         95% CI | t(196) |      p
-----------------------------------------------------------------------
(Intercept) |        4.37 |     0.22 | [ 3.93,  4.82] |  19.49 | < .001
ppgdp       |   -1.30e-05 | 5.37e-06 | [ 0.00,  0.00] |  -2.43 | 0.016 
pctUrban    |       -0.02 | 4.22e-03 | [-0.03, -0.02] |  -5.91 | < .001

Reg. summary: GOF `performance::performance()`

See: easystats/performance

library(performance)
performance(fit1)

# Indices of model performance

AIC     |     BIC |    R2 | R2 (adj.) |  RMSE | Sigma
-----------------------------------------------------
612.669 | 625.842 | 0.315 |     0.308 | 1.106 | 1.114

Reg. summary: `broom`

See: tidymodels/broom

library(broom)
tidy(fit1)

# A tibble: 3 × 5
  term          estimate  std.error statistic  p.value
  <chr>            <dbl>      <dbl>     <dbl>    <dbl>
1 (Intercept)  4.37      0.224          19.5  9.49e-48
2 ppgdp       -0.0000130 0.00000537     -2.43 1.60e- 2
3 pctUrban    -0.0249    0.00422        -5.91 1.51e- 8

glance(fit1)

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.315         0.308  1.11      45.2 7.38e-17     2  -302.  613.  626.
# … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

Fitted values

fitted(fit1)

        1         2         3         4         5         6         7         8 
3.7947689 3.0059609 2.6468172 2.8480812 1.7037141 1.9379459 2.7403669 2.9053011 
        9        10        11        12        13        14        15        16 
1.4119940 2.0911577 3.0052991 1.9886579 1.9199000 3.6430633 3.0641052 2.4314920 
       17        18        19        20        21        22        23        24 
1.3862537 2.9952823 3.3182902 0.6747918 3.4756333 2.6793659 3.0951648 2.7331546 
       25        26        27        28        29        30        31        32 
2.0671501 2.0550740 2.4975767 3.6948524 4.0979139 3.8656137 2.8887204 1.7516254 
       33        34        35        36        37        38        39        40 
2.7874076 1.1388925 3.3968120 3.6672314 2.0020368 3.1216901 2.4246981 3.6671114 
       41        42        43        44        45        46        47        48 
2.7700478 2.3216559 2.6544945 3.0886981 2.7490962 2.4314607 2.2355078 2.2850335 
       49        50        51        52        53        54        55        56 
3.4748106 1.4786284 2.4642316 2.6135811 2.5626587 3.6425976 2.6271288 3.2435170 
       57        58        59        60        61        62        63        64 
2.7103038 3.1579408 3.8205923 2.4460360 3.9465136 3.0325880 1.6762323 1.7159693 
       65        66        67        68        69        70        71        72 
2.7819453 2.0691912 2.8969061 3.0189655 2.0108490 3.0614501 2.4839826 1.8212757 
       73        74        75        76        77        78        79        80 
3.2808694 3.0910653 3.4718507 3.6198606 3.6127258 3.0210259 3.0524099 1.4679432 
       81        82        83        84        85        86        87        88 
2.5121838 1.5201712 3.6085506 3.2147493 2.5373335 2.7184888 2.2267800 1.7000065 
       89        90        91        92        93        94        95        96 
2.2134163 3.0149341 2.1423929 2.3482393 2.7848806 3.7908188 3.2589819 1.3402665 
       97        98        99       100       101       102       103       104 
3.4910499 3.5135847 2.5411568 2.0858293 3.6639271 3.1756366 2.2834597 2.5619918 
      105       106       107       108       109       110       111       112 
0.8857851 1.2309605 3.5964818 3.8713509 2.4464745 3.2917600 3.4447045 1.7519703 
      113       114       115       116       117       118       119       120 
2.5405692 3.3132026 3.2302727 2.3124210 3.7663411 3.1572796 2.7755058 2.7697167 
      121       122       123       124       125       126       127       128 
2.8670865 3.3973768 3.5158206 3.3358407 1.8023346 3.8939496 1.7923763 1.6946431 
      129       130       131       132       133       134       135       136 
2.4935395 1.8095518 2.9146065 3.9460818 3.0875801 2.8729742 1.2778538 2.2844786 
      137       138       139       140       141       142       143       144 
3.4643407 2.1404996 2.5070510 2.4065499 4.0317609 2.7935766 2.3854688 3.1256589 
      145       146       147       148       149       150       151       152 
2.6946634 2.5749830 1.5628115 1.0382976 2.0319552 2.8312421 2.4206636 3.8939809 
      153       154       155       156       157       158       159       160 
3.5896173 3.8323997 2.7880734 2.1249136 3.2895746 2.9123630 2.8298218 3.3981047 
      161       162       163       164       165       166       167       168 
1.3119324 2.7956994 2.8521083 3.8853555 3.4261067 2.7350866 2.0327080 3.9944969 
      169       170       171       172       173       174       175       176 
3.0481549 3.3290636 2.5388828 3.8079068 1.6187754 1.6322415 2.9409538 3.7158988 
      177       178       179       180       181       182       183       184 
3.6949007 2.8466123 3.4670765 3.2712912 3.7301469 3.8271317 2.6251786 2.4987419 
      185       186       187       188       189       190       191       192 
3.0688209 3.0621762 4.0437545 2.6157528 1.7647646 1.9074322 1.6993888 1.9015464 
      193       194       195       196       197       198       199 
3.4588083 3.6878846 1.8564110 3.5865571 3.5583256 3.4612803 3.3952165

Residuals

resid(fit1)

          1           2           3           4           5           6 
 2.17323111 -1.48096095 -0.50481721  2.28691883  0.29628594  0.23405405 
          7           8           9          10          11          12 
-1.00536689 -1.23430108  0.53700600 -0.74515772 -0.85729906 -0.11165790 
         13          14          15          16          17          18 
 0.51009998 -1.48606333 -1.48910516 -0.95249201  0.44874633 -0.31628228 
         19          20          21          22          23          24 
 1.75970984  1.08520825 -1.21763328  0.54963411 -1.96116482 -0.11615458 
         25          26          27          28          29          30 
-0.26715012 -0.07107397 -0.95157666  2.05514757 -0.04691388 -1.44361367 
         31          32          33          34          35          36 
 1.39827962 -0.06062539 -0.50840760  0.46110747  1.02618805  2.06976863 
         37          38          39          40          41          42 
-0.17003681 -1.56269009 -0.13169815  1.07488865  1.67195223  0.20915040 
         43          44          45          46          47          48 
-0.84249451  1.13530190 -1.24809620 -0.98046070 -0.77750782 -0.78403353 
         49          50          51          52          53          54 
 2.01018936  0.40637164  1.12476835  0.38641894 -0.07265866  2.27540238 
         55          56          57          58          59          60 
-0.23412884 -0.60751700 -0.53930380  1.82205918  0.42240766 -0.74403600 
         61          62          63          64          65          66 
-0.09851358 -0.43058797  0.19876769  0.27103069 -0.74894529  1.12580884 
         67          68          69          70          71          72 
 1.79209386 -1.49096555 -0.55384897  0.92654987 -0.94398258  0.39572432 
         73          74          75          76          77          78 
-1.10986945  0.74893473  1.56014928  1.25713938 -1.42272578  0.13797414 
         79          80          81          82          83          84 
-0.05640991 -0.33094322 -1.08218377  0.57782878 -1.07055057 -1.15974928 
         85          86          87          88          89          90 
-0.95033352  1.81651124 -0.12978005  1.20899348 -0.73741634 -0.75293412 
         91          92          93          94          95          96 
-0.72439291  0.54076072 -0.30388056  0.83218115  0.24101810  0.91073351 
         97          98          99         100         101         102 
-0.87004991 -0.97058471 -1.03515681 -0.32182931 -0.61292706  1.86236345 
        103         104         105         106         107         108 
 0.12654028 -1.06699184  0.79721493 -0.06796051  0.89651819  2.09664912 
        109         110         111         112         113         114 
 0.12552547 -1.62375995  2.67229550 -0.46797035  1.84389706  1.04779741 
        115         116         117         118         119         120 
-1.64027267 -0.08542101 -0.45934113 -1.70727957 -0.32950581 -1.13971671 
        121         122         123         124         125         126 
-0.68408649  1.31562320 -1.57682063 -0.28084074  1.49766544 -1.30694960 
        127         128         129         130         131         132 
 0.10762365  0.09935694 -0.40253945  0.32544818 -0.41460645  2.97891821 
        133         134         135         136         137         138 
 2.34341986 -0.88497422  0.67014618 -0.13847861 -0.26334069 -0.14049955 
        139         140         141         142         143         144 
 1.76294902  0.00245011 -0.23276089  0.06442340  0.02453119 -0.07565890 
        145         146         147         148         149         150 
-1.27966338 -1.26298297  0.19418853  1.16570241 -0.64295518 -1.40324213 
        151         152         153         154         155         156 
-0.89166361  1.38801909 -1.68261729 -0.06939970  0.69992660  0.51408637 
        157         158         159         160         161         162 
 1.31542538 -1.35036300 -0.48982181  1.32989528  0.05506763 -1.42369940 
        163         164         165         166         167         168 
-1.37510833  0.15564447  2.85689331 -0.35208655 -0.52870796 -1.75949694 
        169         170         171         172         173         174 
-1.05315491  0.89593645 -0.27288277 -0.63390684  0.30622457 -0.09624147 
        175         176         177         178         179         180 
-0.16895381 -0.55389879  1.80409931 -1.44961230 -1.93907653  0.59270880 
        181         182         183         184         185         186 
 0.05285313 -2.19513168 -0.71617861 -0.47674187 -0.75282087  0.63782377 
        187         188         189         190         191         192 
 1.85724550 -1.13275277 -0.05776457 -0.04043224  0.37761115  0.14145363 
        193         194         195         196         197         198 
-1.19480829  0.06211543  0.53458896 -1.83655714  1.37967443  2.83871967 
        199 
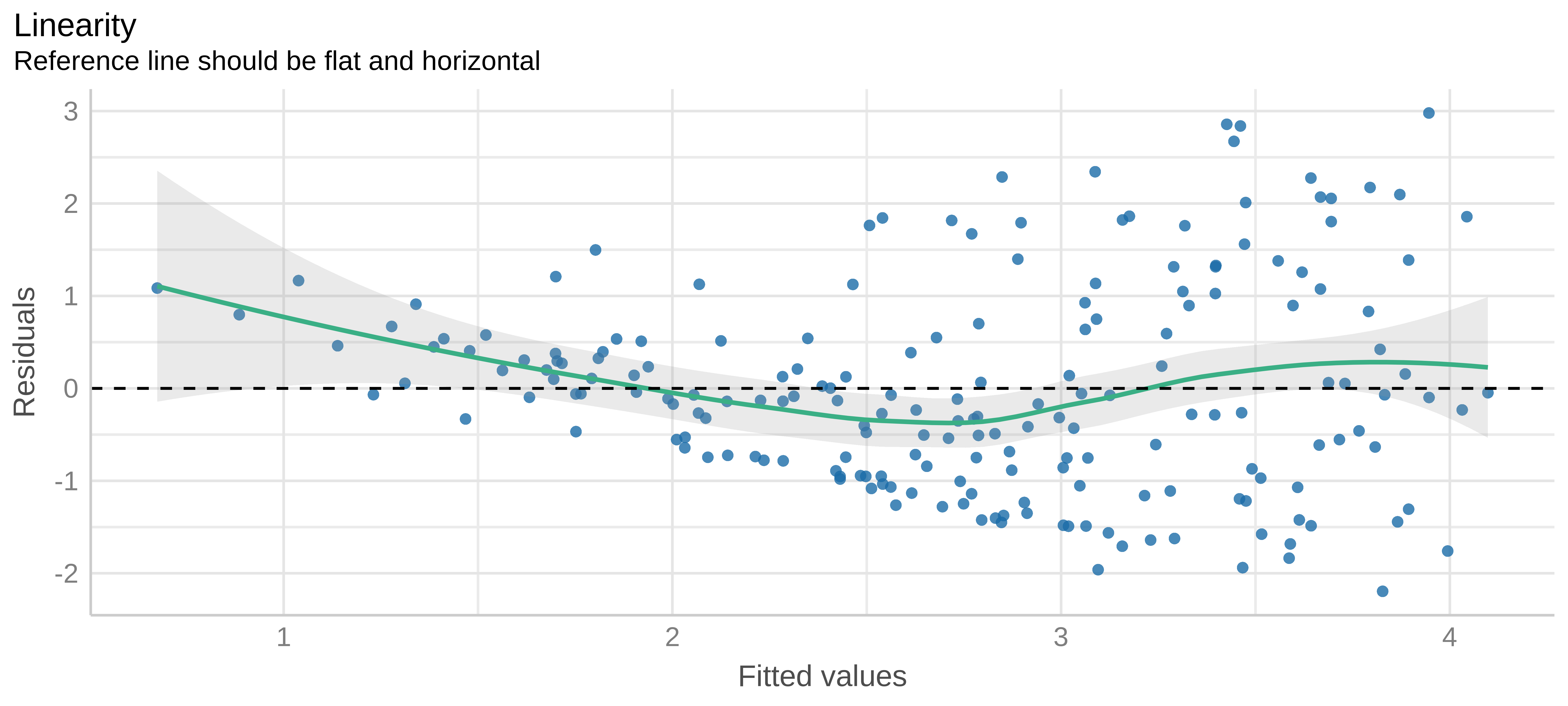
-0.28621654

Residuals vs Fitted

See: easystats/performance + check_model help

Code

check_model(fit1, check = "linearity", panel = FALSE)

$NCV

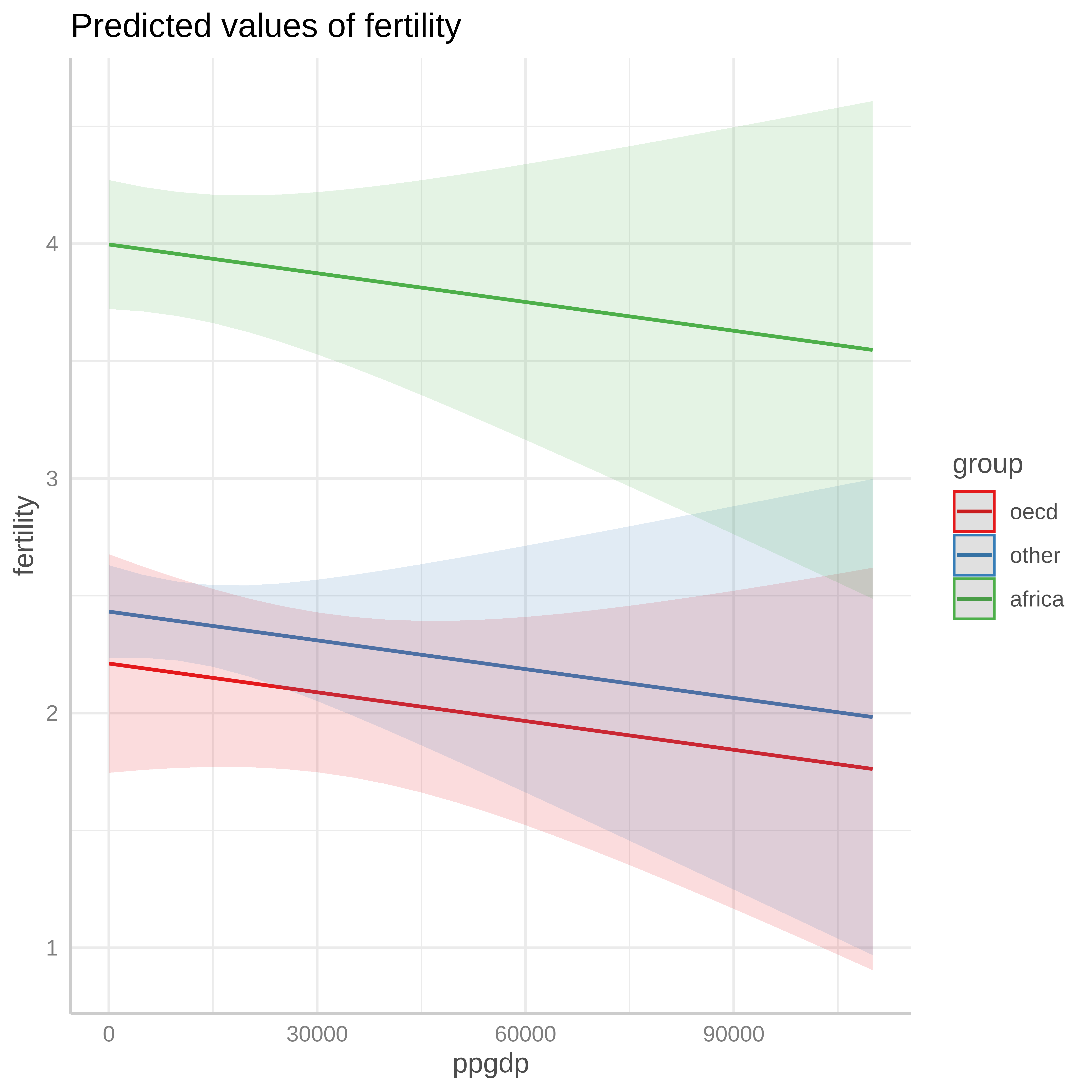
Predicted values

See: strengejacke.github.io/ggeffects

Code

library(ggeffects)
ggpredict(fit1, terms = "ppgdp")

# Predicted values of fertility

 ppgdp | Predicted |       95% CI
---------------------------------
     0 |      2.93 | [2.72, 3.14]
 15000 |      2.74 | [2.58, 2.89]
 25000 |      2.60 | [2.41, 2.80]
 40000 |      2.41 | [2.09, 2.73]
 55000 |      2.21 | [1.75, 2.68]
 70000 |      2.02 | [1.40, 2.64]
 85000 |      1.82 | [1.05, 2.60]
110000 |      1.50 | [0.46, 2.53]

Adjusted for:
* pctUrban = 57.93

Code

fit2 <- lm(fertility ~ ppgdp + pctUrban + group, un_dta)
ggpredict(fit2, terms = c("ppgdp", "group")) %>% plot()

Application Exercise 1: Multiple regression with a dummy variable

AE04-01 Multiple Linear Regression

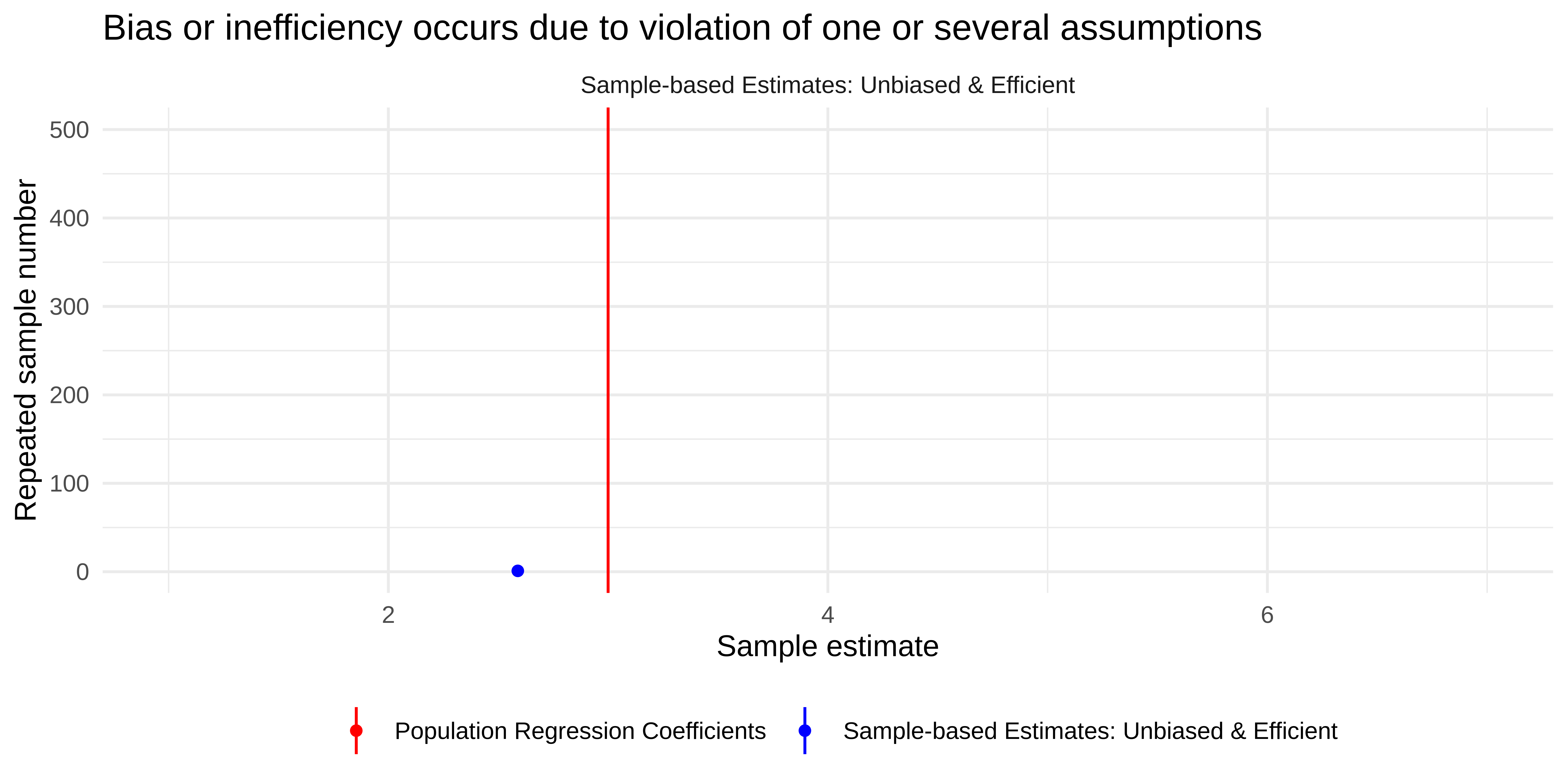
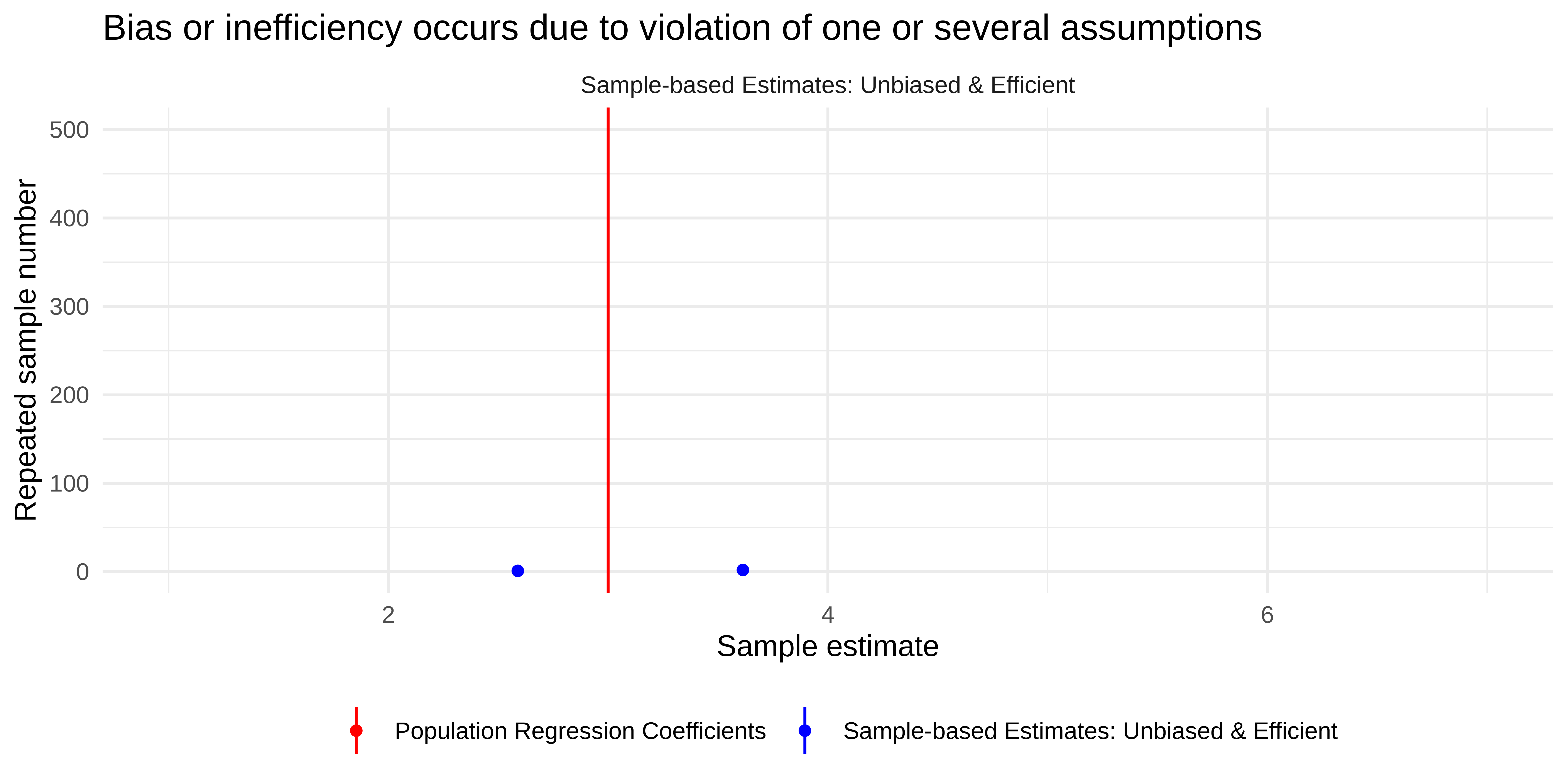
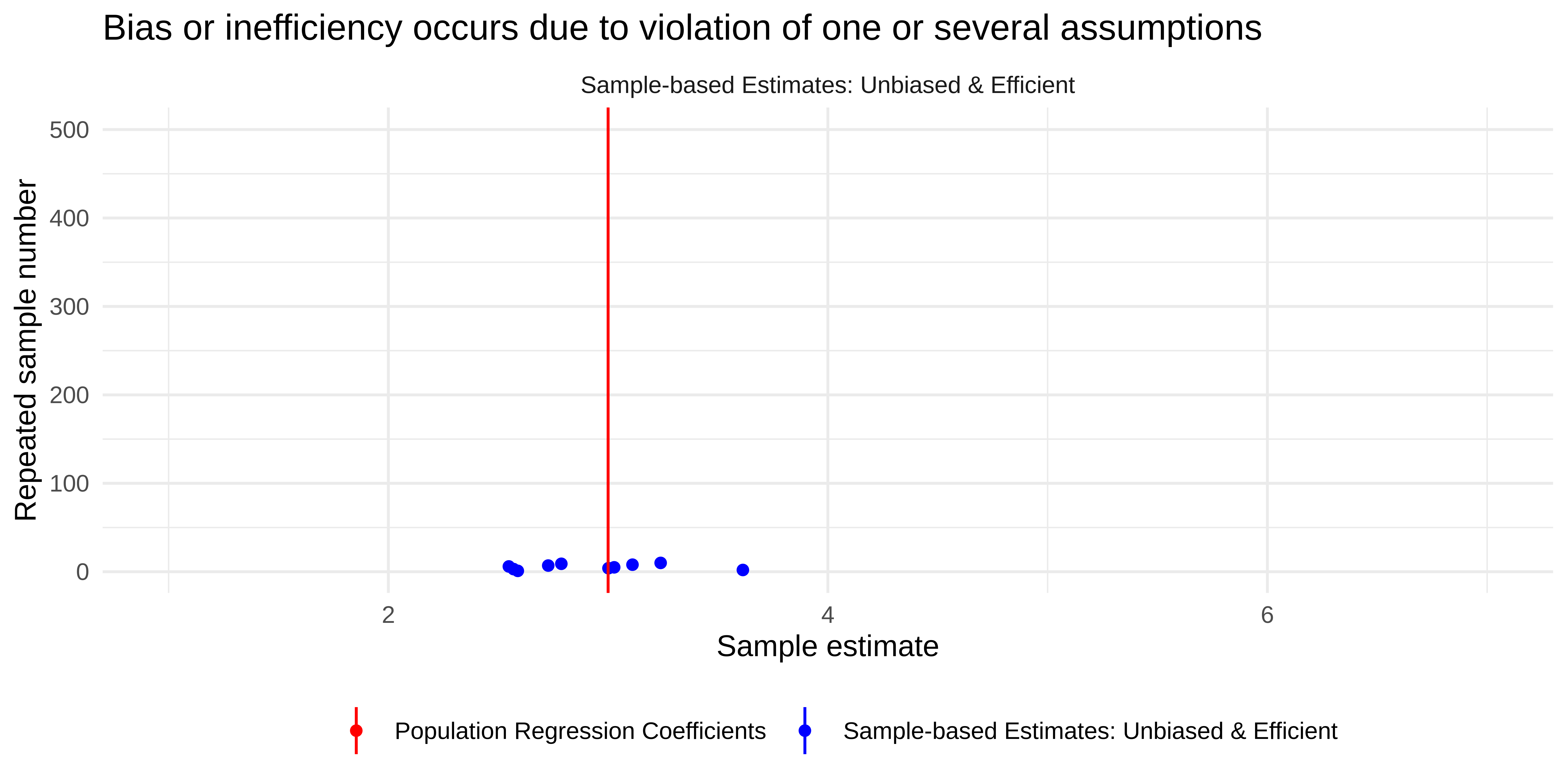
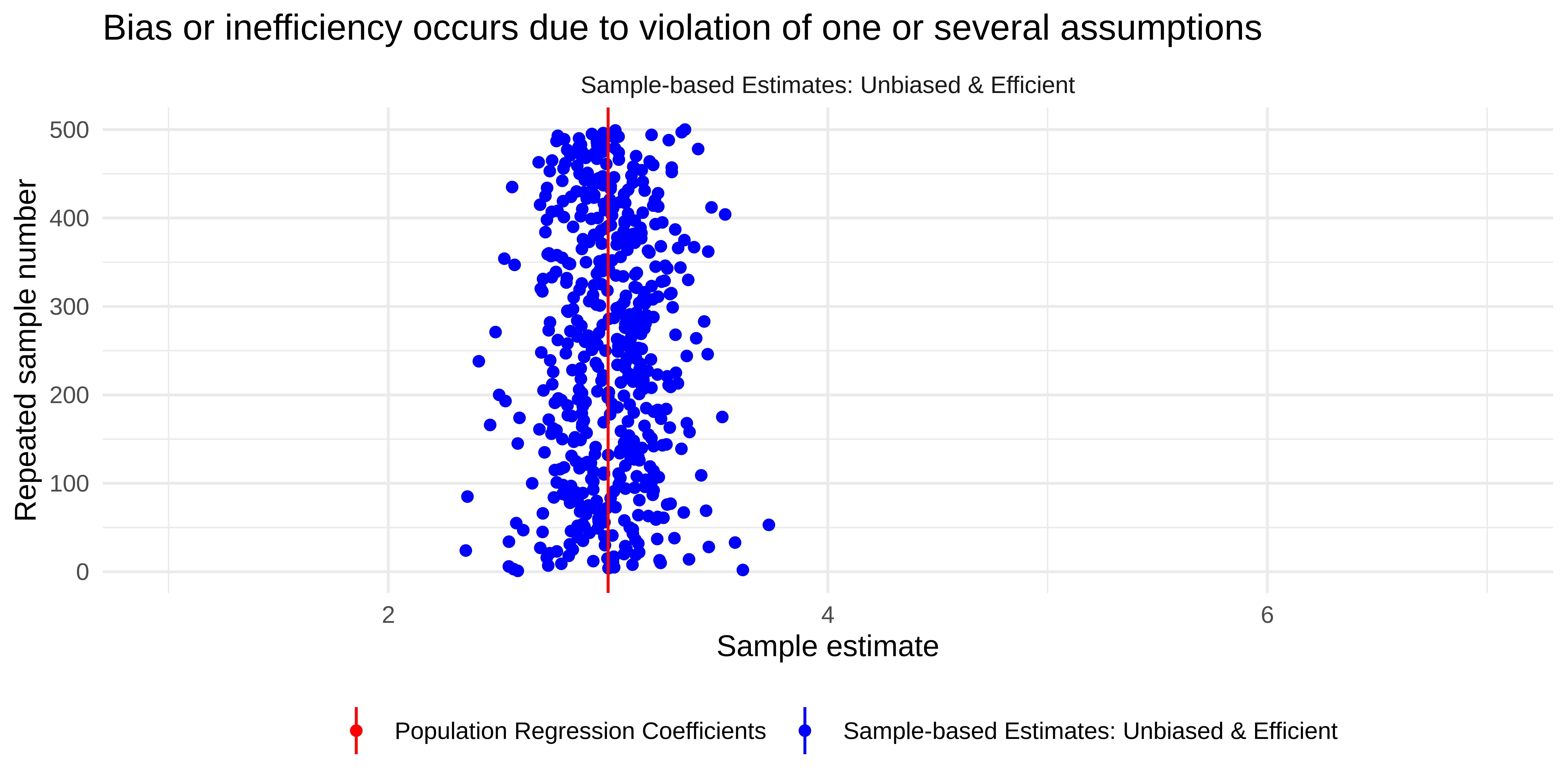
Bias and Efficiency

… of estimates

Sampling from the population

Unbiased but inefficient

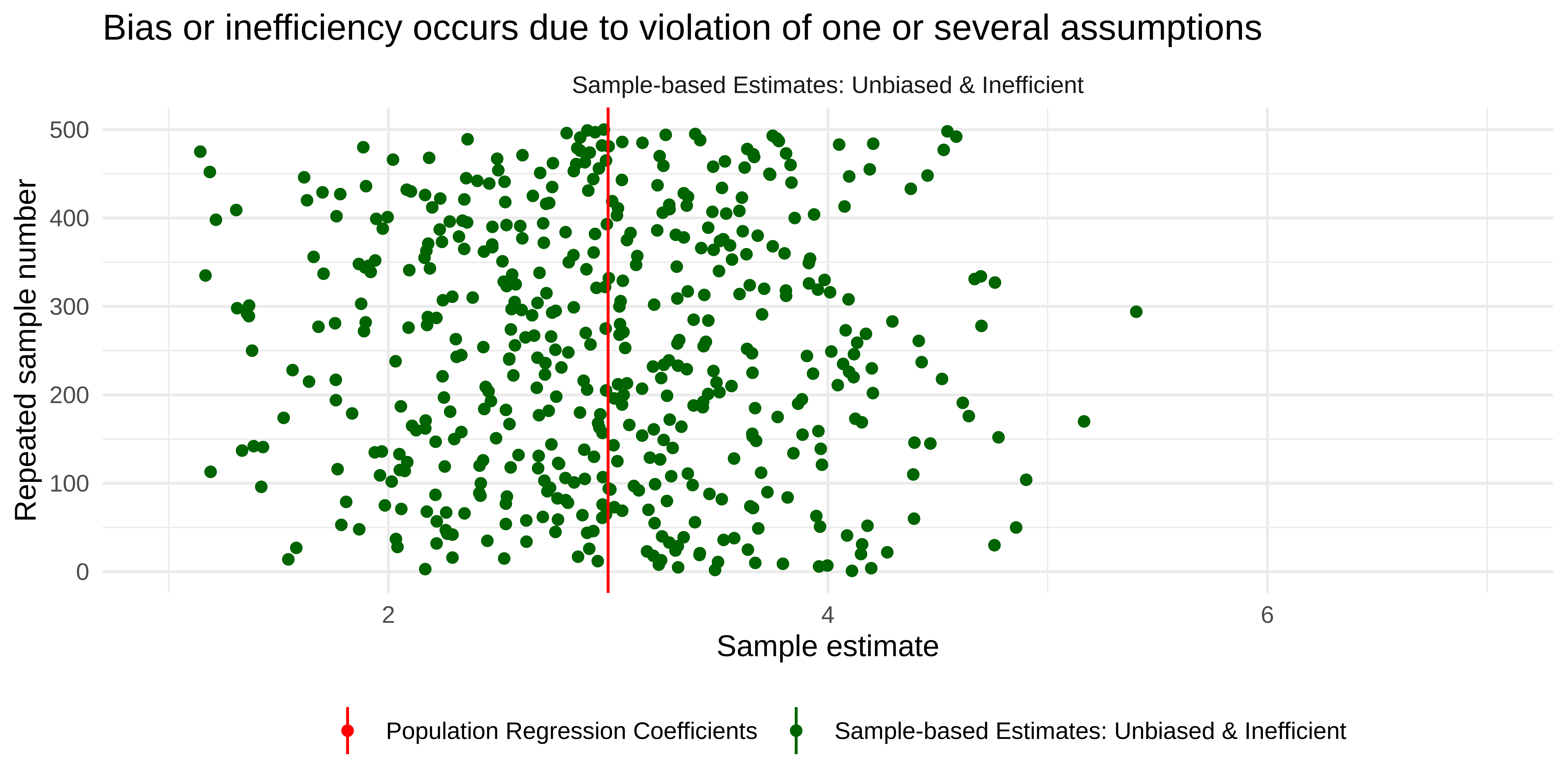
Biased but efficient

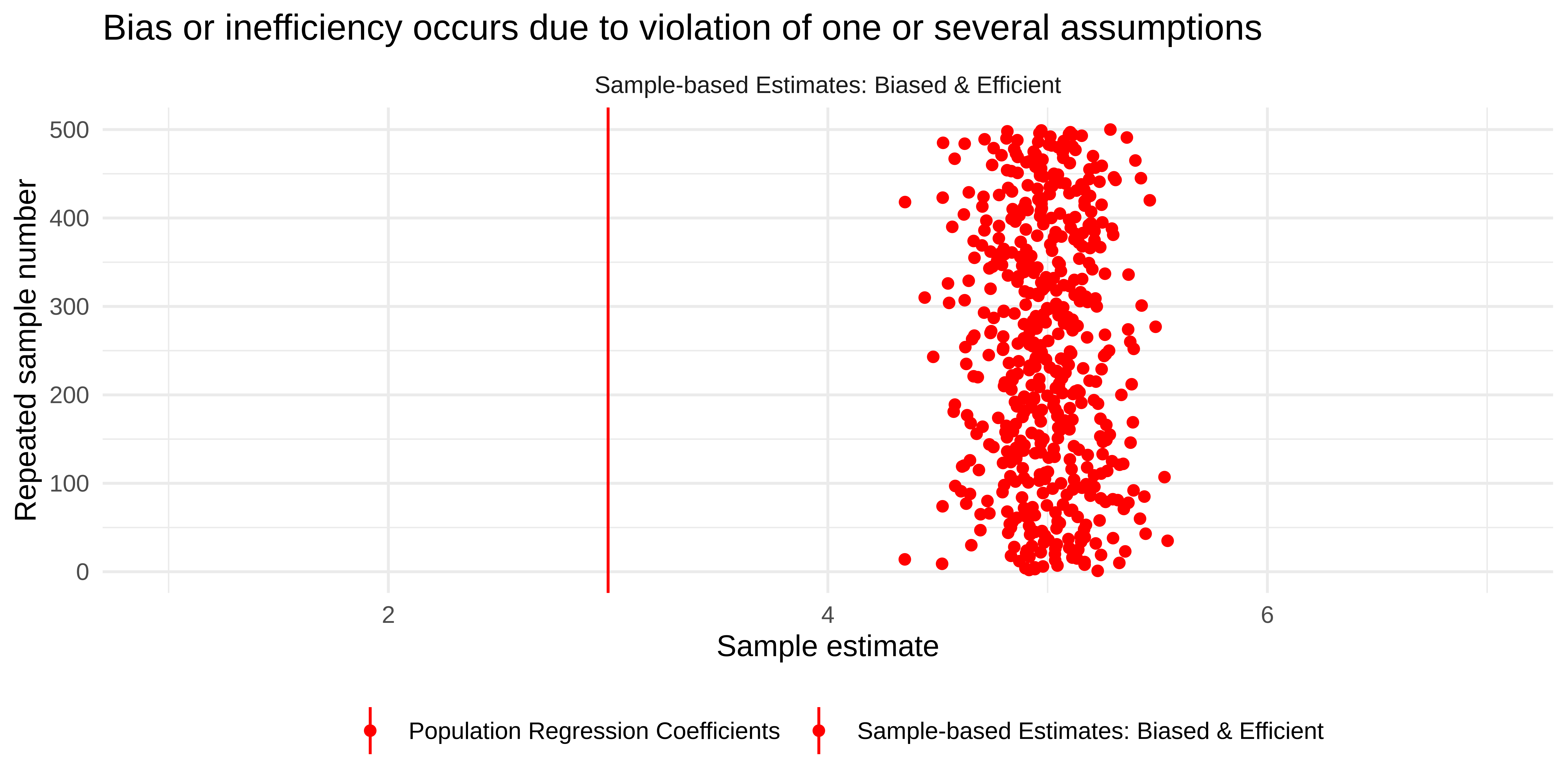
Biased and inefficient

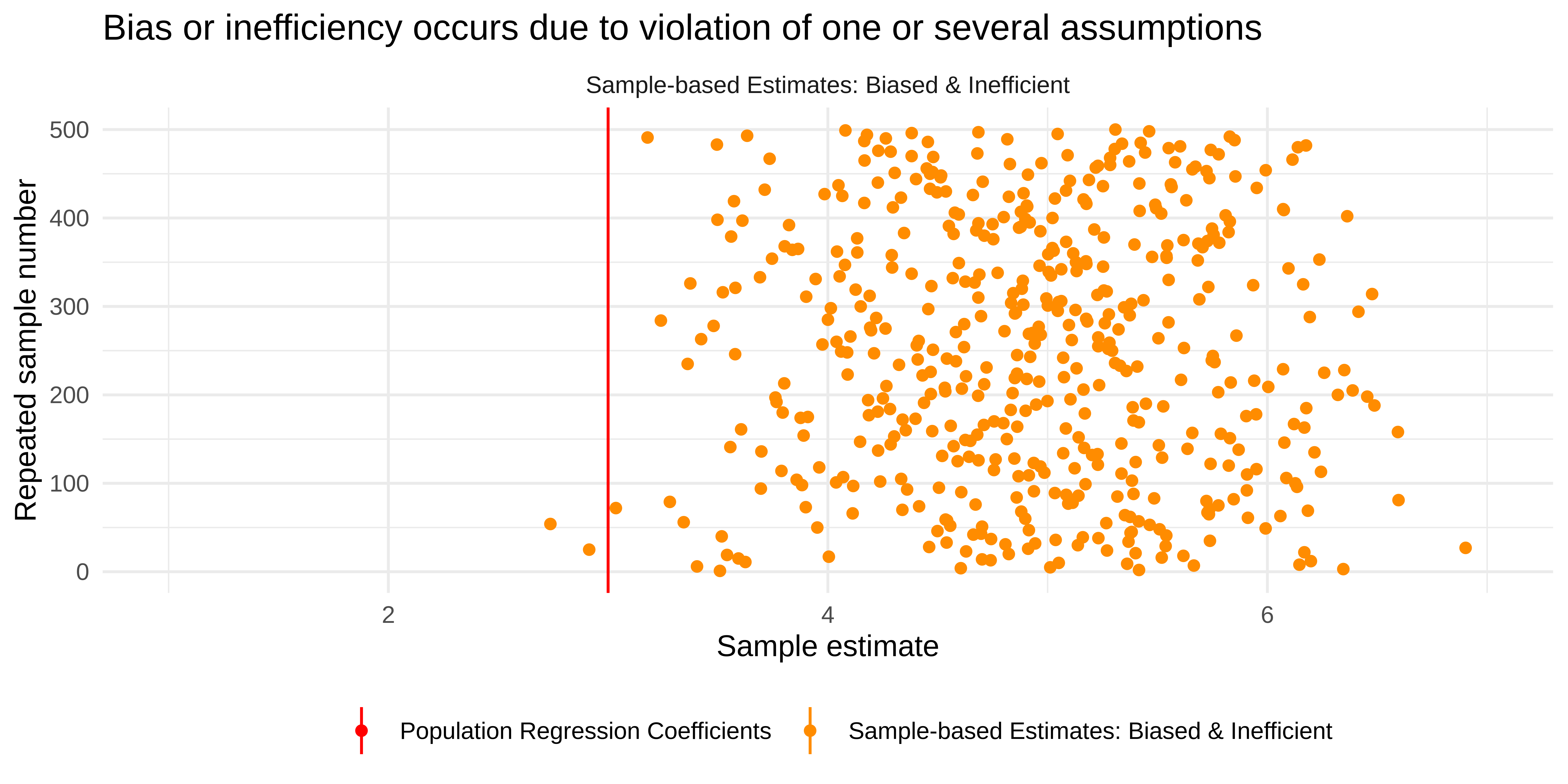
All four cases

Assumptions of the MLR

Assumptions? What? Why? BLUE?

OLS is unbiased (Gauss-Markov Theorem), when assumptions 1 to 4 are satisfied:
1. Linearity
2. Random Sampling
3. No Collinearity
4. No Endogeneity
OLS is BLUE (Gauss-Markov Theorem). AKA (Best Linear Unbiased Estimator or unbiased and efficient), when assumptions 1 to 4 + 5 are satisfied
1. Homoscedasticity (No Autocorrelation)
OLS is a Classical linear model (CLM), when assumptions 1 to 5 + 6 are satisfied
1. Error Terms Normality

Multiple linear regression: recap

Overview

\[y = \hat {\beta}_{0} + \hat {\beta}_{1}x_1 + \hat {\beta}_{2}x_2 + \hat {\beta}_{3}x_3 + \cdots + \hat {\beta}_{k}x_k + \hat u\]

\(\hat u\) - Error term, or disturbance containing factors other than \(x_1, x_2, \cdots, x_k\) that affect \(y\)
\(\hat {\beta}_{0}\) - intercept (constant term);
\(\hat {\beta}_{1}\), \(\hat {\beta}_{2}\), \(\hat {\beta}_{k}\) - coefficients / parameters associated with \(x_1\), \(x_2\), … \(x_k\);
\(k\) - entire set of independent variables;

Motivation

To incorporate more explanatory factors into a model;
Explicitly hold fixed (some) other factors;
Allow for more flexible functional forms;

Interpretation

The multiple linear regression shows the effect of each variable, holding other explanatory variables fixed;

Important

We assume that all unobserved factors do not change if the explanatory variables are changed.

Examples of the multiple regression

1. Wage equation

2. Average test scores and per student spending

3. Family income and family consumption

two explanatory variables;
consumption is explained as a quadratic function of income;
great care when when interpreting the coefficients;

4. CEO salary, sales and CEO tenure

Model assumes a constant elasticity relationship between CEO salary and the sales of his or her firm.
Model assumes a quadratic relationship between CEO salary and his or her tenure with the firm.

Weisberg, Sanford. 2005. Applied Linear Regression. John Wiley & Sons, Inc. https://doi.org/10.1002/0471704091.

Multiple Lnear Regression

R setup

Example 1: UN11 data

Research question

Data loading

Descriptive statistics

Data visualization

Regression

Reg. summary base R

Reg. summary; Coef. parameters::parameters()

Reg. summary: GOF performance::performance()

Reg. summary: broom

Fitted values

Residuals

Residuals vs Fitted

Predicted values

Application Exercise 1: Multiple regression with a dummy variable

Bias and Efficiency

… of estimates

Sampling from the population

Unbiased and efficient

Unbiased but inefficient

Biased but efficient

Biased and inefficient

All four cases

Assumptions of the MLR

Assumptions? What? Why? BLUE?

Multiple linear regression: recap

Overview

Motivation

Interpretation

Examples of the multiple regression

1. Wage equation

2. Average test scores and per student spending

3. Family income and family consumption

4. CEO salary, sales and CEO tenure

Reg. summary `base` R

Reg. summary; Coef. `parameters::parameters()`

Reg. summary: GOF `performance::performance()`

Reg. summary: `broom`