library(tidyverse) # for data wrangling
library(alr4) # for the data sets #
library(GGally)
library(ggpmisc)
library(parameters)
library(performance)
library(see)
library(car)
library(broom)
library(modelsummary)
library(texreg)
ggplot2::theme_set(ggplot2::theme_bw())
knitr::opts_chunk$set(
fig.width = 12,
fig.asp = 0.618,
fig.retina = 3,
dpi = 300,
out.width = "100%",
message = FALSE,
echo = TRUE,
cache = TRUE
)
my_gof <- function(fit_obj, digits = 4) {
sum_fit <- summary(fit_obj)
stars <-
pf(sum_fit$fstatistic[1],
sum_fit$fstatistic[2],
sum_fit$fstatistic[3],
lower.tail=FALSE) %>%
symnum(corr = FALSE, na = FALSE,
cutpoints = c(0, .001,.01,.05, 1),
symbols = c("***","**","*"," ")) %>%
as.character()
list(
# `R^2` = sum_fit$r.squared %>% round(digits),
# `Adj. R^2` = sum_fit$adj.r.squared %>% round(digits),
# `Num. obs.` = sum_fit$residuals %>% length(),
`Num. df` = sum_fit$df[[2]],
`F statistic` =
str_c(sum_fit$fstatistic[1] %>% round(digits), " ", stars)
)
}
screen_many_regs <-
function(fit_obj_list, ..., digits = 4, single.row = TRUE) {
if (class(fit_obj_list) == "lm")
fit_obj_list <- list(fit_obj_list)
if (length(rlang::dots_list(...)) > 0)
fit_obj_list <- fit_obj_list %>% append(rlang::dots_list(...))
# browser()
fit_obj_list %>%
screenreg(
custom.note =
map2_chr(., seq_along(.), ~ {
str_c("Model ", .y, " ", as.character(.x$call)[[2]])
}) %>%
c("*** p < 0.001; ** p < 0.01; * p < 0.05", .) %>%
str_c(collapse = "\n") ,
digits = digits,
single.row = single.row,
custom.gof.rows =
map(., ~my_gof(.x, digits)) %>%
transpose() %>%
map(unlist),
reorder.gof = c(3, 4, 5, 1, 2)
)
}Linearity
MP223 - Applied Econometrics Methods for the Social Sciences
Eduard Bukin
R setup
Linearity
Linearity: meaning
the expected value of dependent variable is a straight-line function of the independent variable
If linearity is violated:
- bias of our estimates
- inappropriate representation of the dependent variable
Linearity: detection
How to detect a non-linearity?
- no accepted statistical tests, but
- less known Tukey test
- visual inspection
Typical plots:
- Scatter plots of dependent and independent variables;
- observed versus predicted/fitted values;
- residuals versus predicted/fitted values;
Linearity: resolutions
(non) linear transformation to the dependent and/or independent variables;
- it does change the way how we must interpret coefficients;
find a different independent variable;
propose a different functional form;
Common linear transformations

Power transformation or Box-Cox transformations;
Variables normalization to the standard normal distribution;
Tailor expansion (Cobb-Douglas, Trans-log)
Examples
Example 1: Anscombe quartet
Descriptive statistics
Four data sets each of 11 observations and two variables (x and y).
Descriptive statistics:
Code
anscombe %>%
mutate(id = row_number()) %>%
pivot_longer(c(contains("x"), contains("y")), names_to = "Variables") %>%
mutate(`Data set` = str_extract(Variables, "\\d"),
Variables = str_remove(Variables, "\\d")) %>%
pivot_wider(names_from = Variables, values_from = value) %>%
group_by(`Data set`) %>%
summarise(across(c(x, y), ~ mean(.), .names = "mean_{.col}"),
across(c(x, y), ~ sd(.), .names = "sd_{.col}"))# A tibble: 4 × 5
`Data set` mean_x mean_y sd_x sd_y
<chr> <dbl> <dbl> <dbl> <dbl>
1 1 9 7.50 3.32 2.03
2 2 9 7.50 3.32 2.03
3 3 9 7.5 3.32 2.03
4 4 9 7.50 3.32 2.03Simple regressions of y on x
# A tibble: 8 × 6
`Data set` term estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 Data set 1 (Intercept) 3.00 1.12 2.67 0.0257
2 Data set 1 x 0.500 0.118 4.24 0.00217
3 Data set 2 (Intercept) 3.00 1.13 2.67 0.0258
4 Data set 2 x 0.5 0.118 4.24 0.00218
5 Data set 3 (Intercept) 3.00 1.12 2.67 0.0256
6 Data set 3 x 0.500 0.118 4.24 0.00218
7 Data set 4 (Intercept) 3.00 1.12 2.67 0.0256
8 Data set 4 x 0.500 0.118 4.24 0.00216Scatter plots
Code
fig_norm_anscombe <-
norm_anscombe %>%
mutate(data_sample = str_c("Data set ", data_sample))
fig_norm_anscombe %>%
ggplot() +
aes(x, y, group = data_sample) +
geom_point() +
geom_smooth(
data = filter(fig_norm_anscombe, data_sample == "Model 2"),
method = "lm",
formula = y ~ x + I(x ^ 2)
) +
geom_smooth(
data = filter(fig_norm_anscombe,
data_sample == "Model 3", y < 11)
) +
geom_abline(slope = 0.5, intercept = 3, colour = "red") +
theme_bw() + facet_wrap(. ~ data_sample) 
Residuals vs fitted
Example 2: Wage and Education
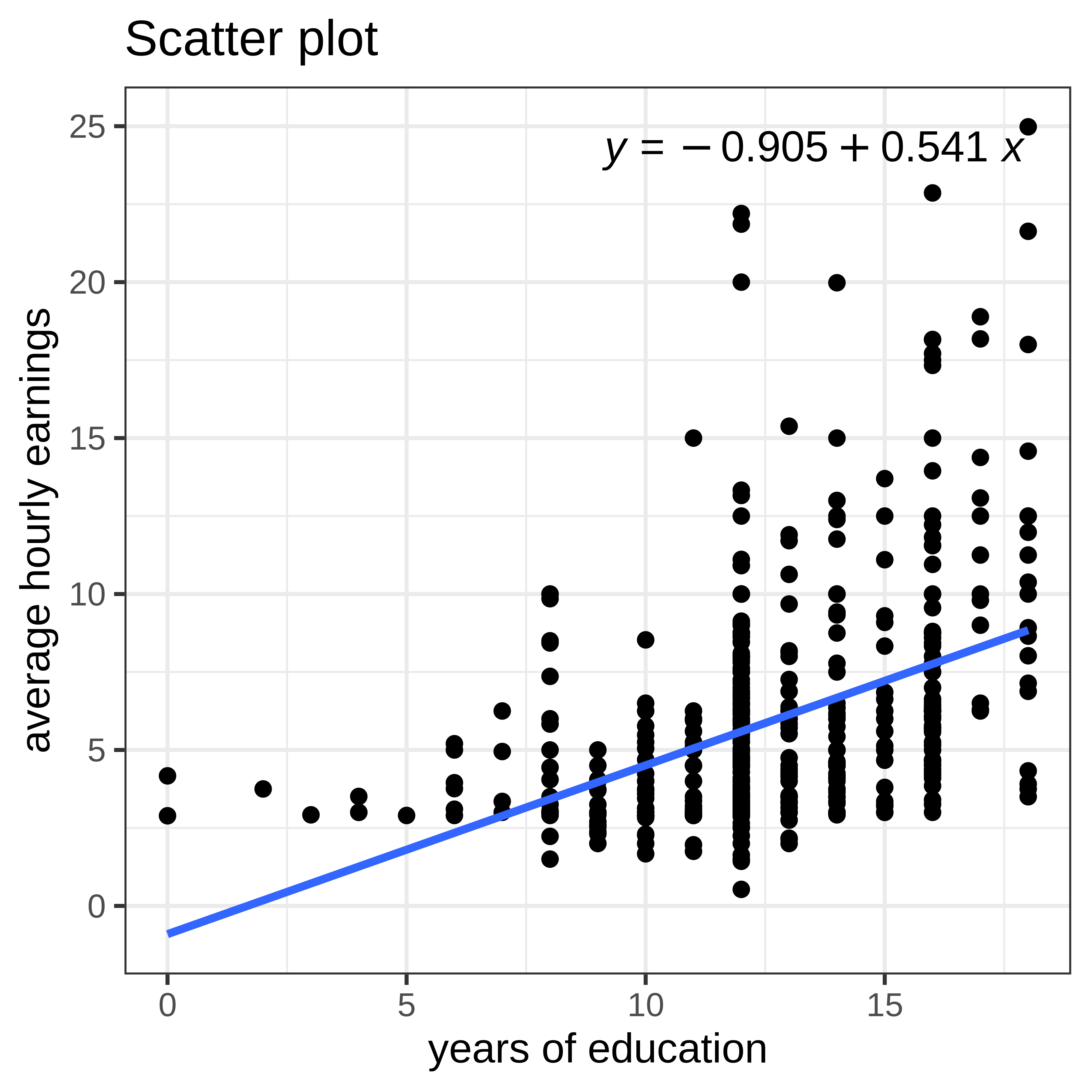
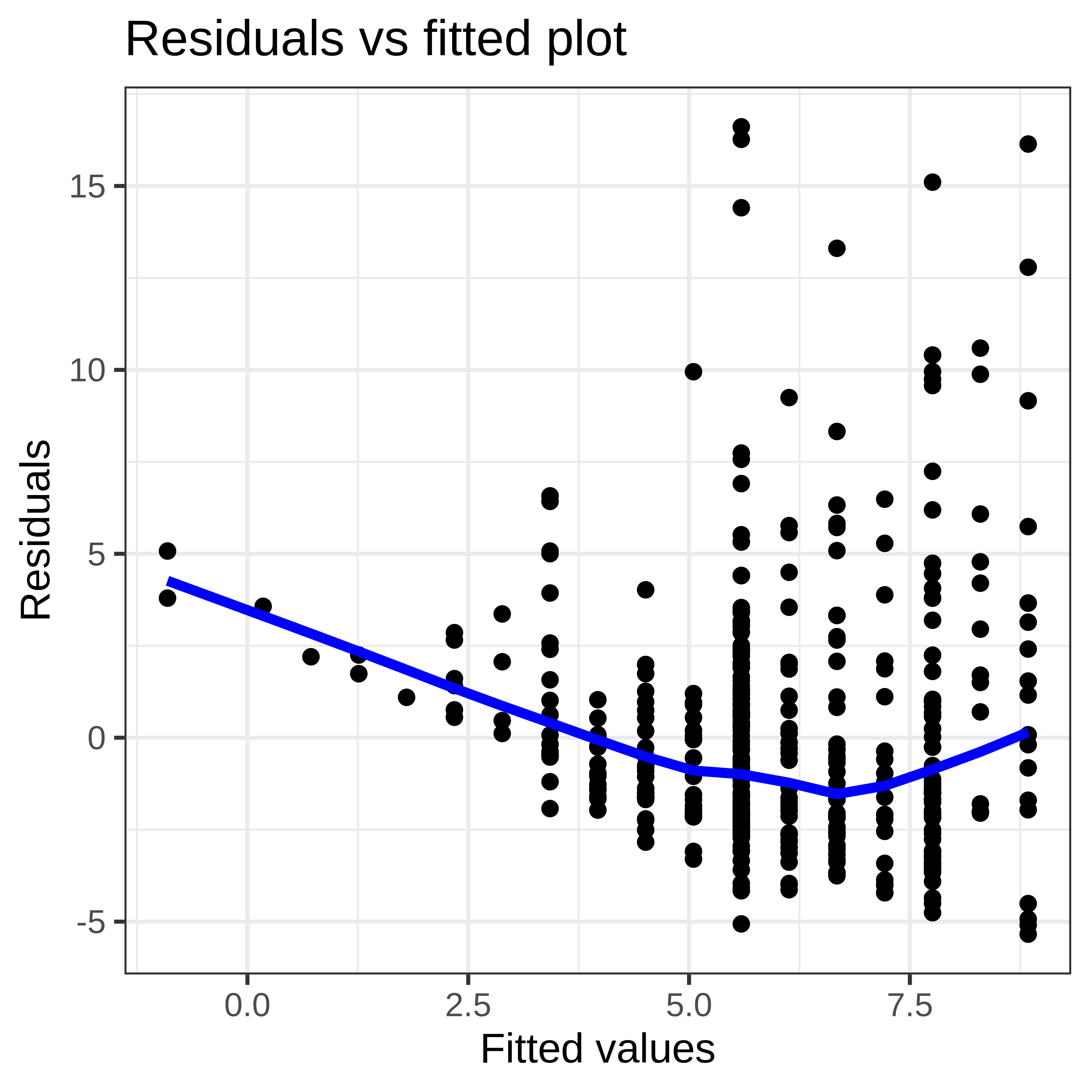
Example 3: Sales and CEO salary
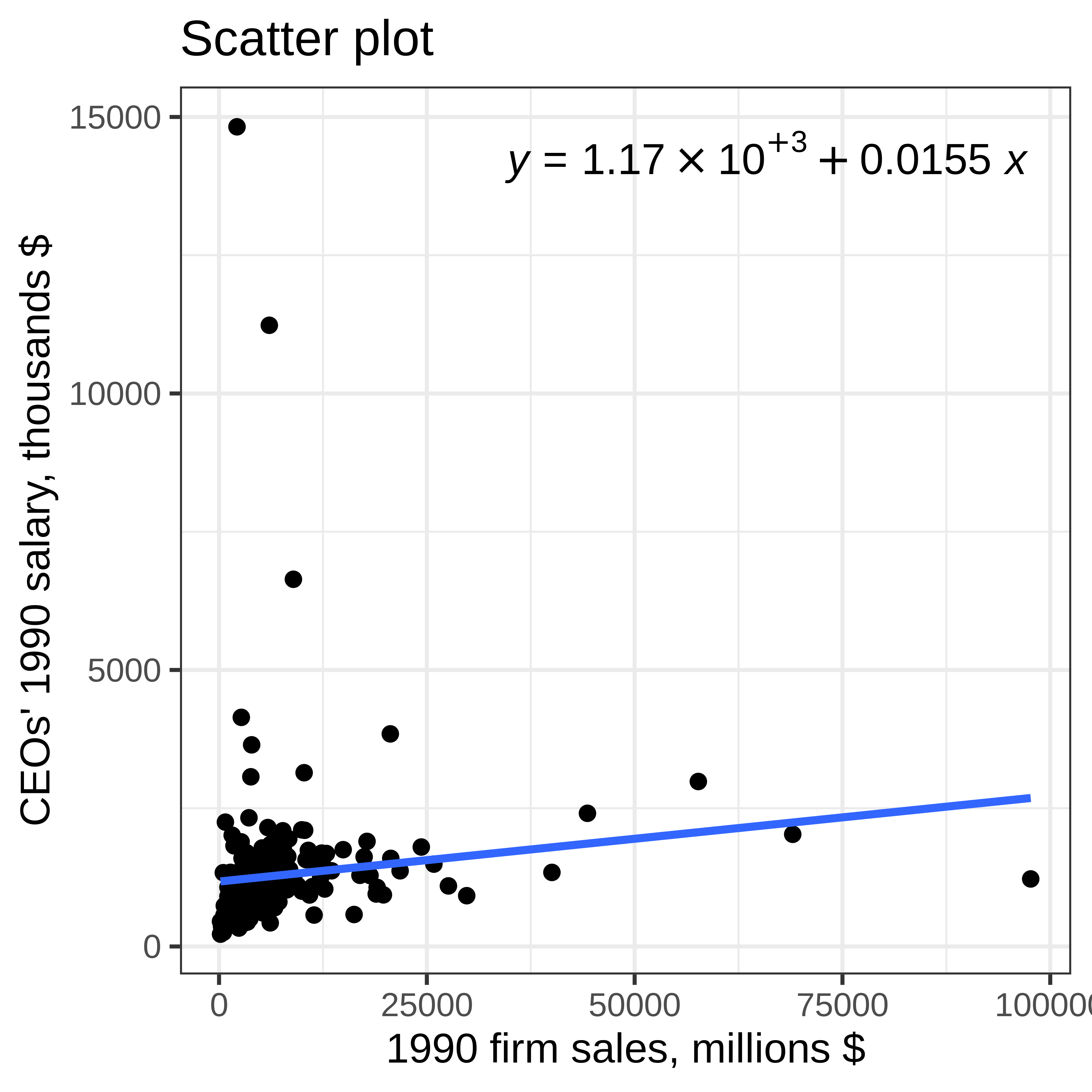
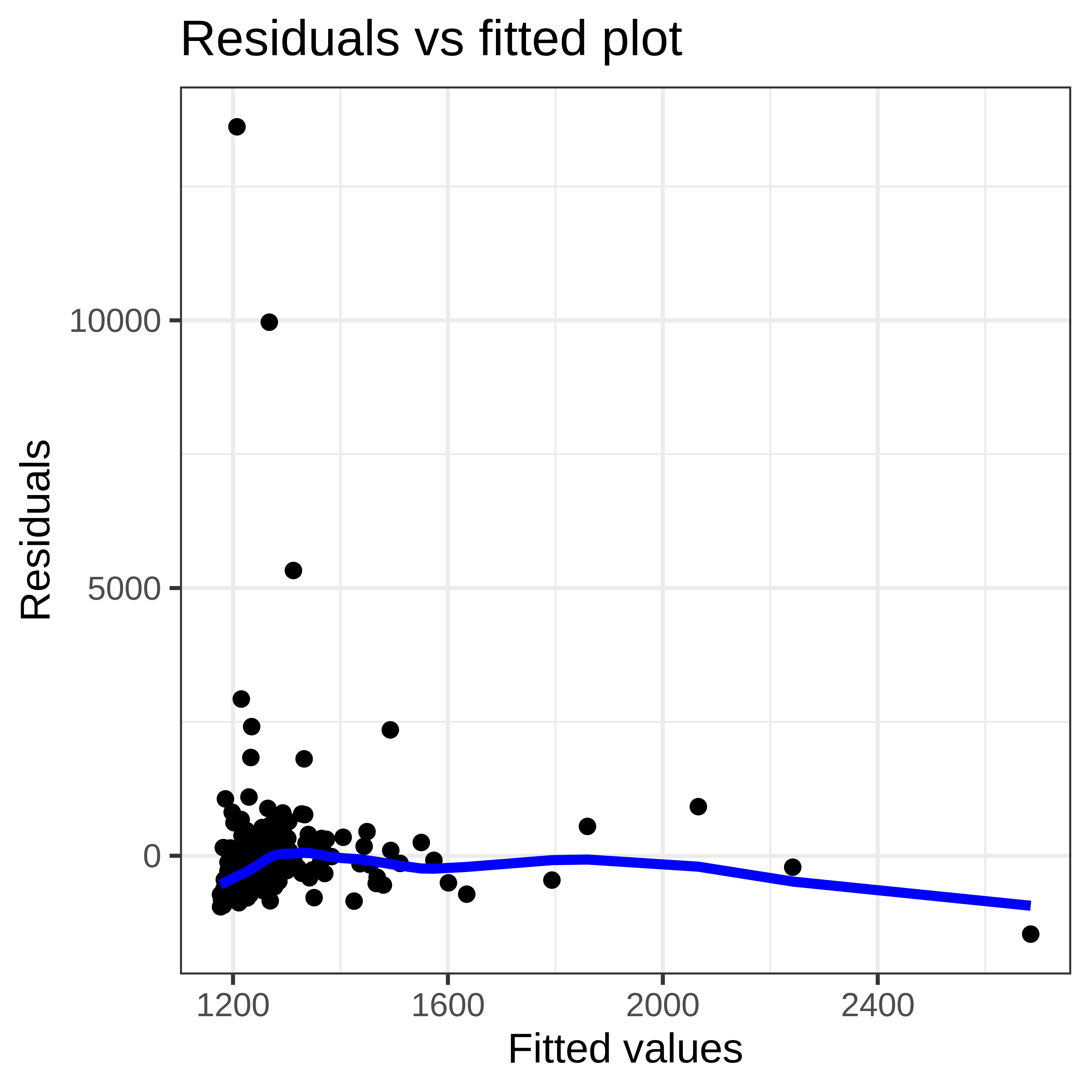
Example 4: Acceptable linearity
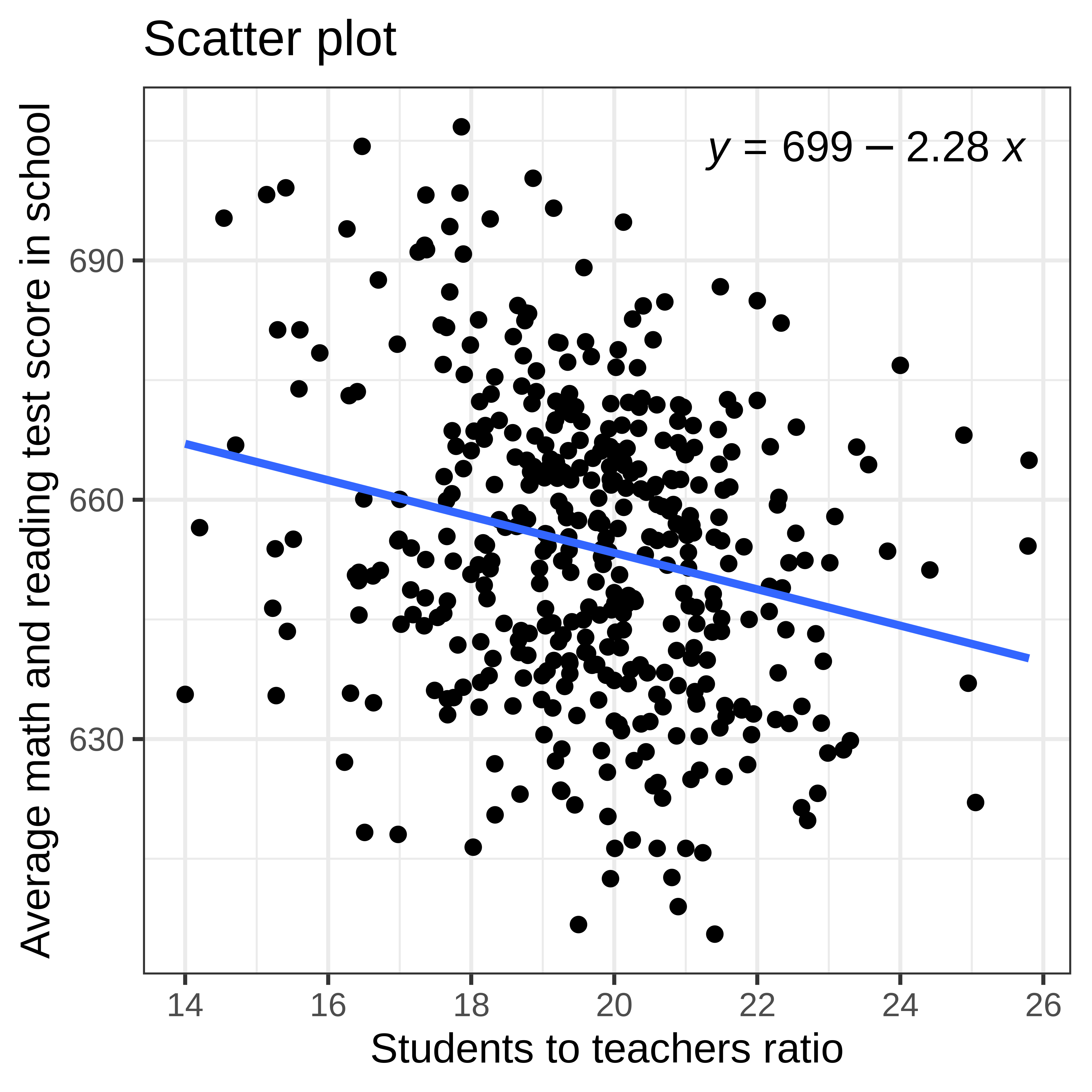
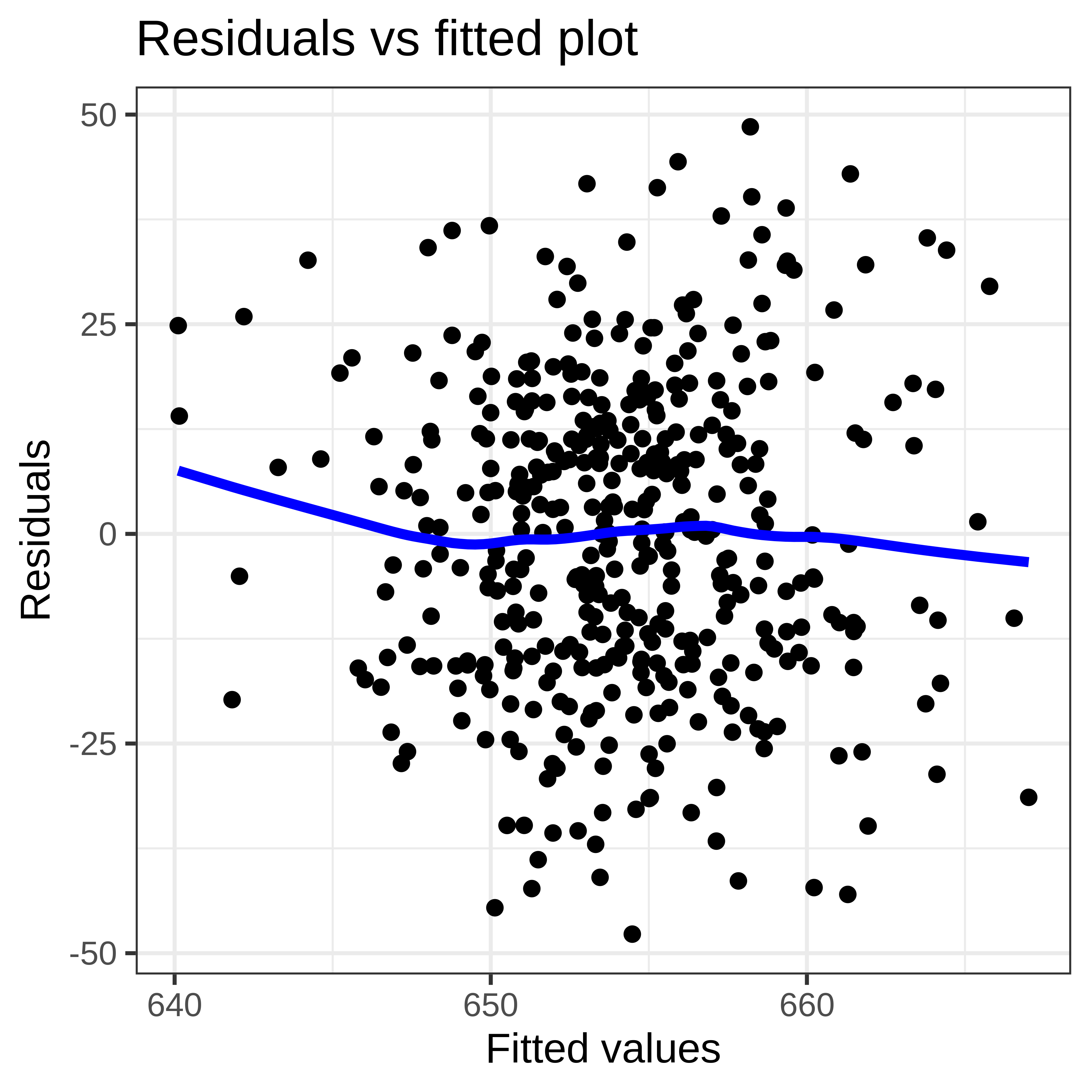
Example 5: Fuel taxes influence on fuel consumption?
As a federal policy maker, we would like to understand how fuel taxes were affecting the gasoline consumption across the states.
We use data on fuel consumption in 2001 across all states in the USA (each observation represents a state). Data from (weisberg2013a?).
Variables present in the data are:
- \(\text{Tax}\) : Gasoline state tax rate, cents per gallon;
- \(\text{Dlic}\) : The number of licensed drivers per 1000 population over the age of 16;;
- \(\text{Income}\) : in 1000 USD Per capita personal income (year 2000);
- \(\text{Miles}\) : Miles of Federal-aid highway miles in the state;
- \(\text{Fuel}\) : Gasoline consumption per capita (gal.);
Empirical model and ex-ante expectations
Regression equation:
- \(\text{Fuel} = \hat\beta_0 + \hat\beta_1 \cdot \text{Tax} + \hat\beta_2 \cdot \text{Dlic} \\ + \hat\beta_3 \cdot \text{Income} + \hat\beta_4 \cdot \text{Miles} + \hat{u}\)
What could be expected values of the coefficients?
Data
Code
Rows: 51
Columns: 5
$ Tax <dbl> 18.0, 8.0, 18.0, 21.7, 18.0, 22.0, 25.0, 23.0, 20.0, 13.6, 7.5,…
$ Dlic <dbl> 1031.3801, 1031.6411, 908.5972, 946.5706, 844.7033, 989.6062, 9…
$ Income <dbl> 23.471, 30.064, 25.578, 22.257, 32.275, 32.949, 40.640, 31.255,…
$ Miles <int> 94440, 13628, 55245, 98132, 168771, 85854, 20910, 5814, 1534, 1…
$ Fuel <dbl> 690.2644, 514.2792, 621.4751, 655.2927, 573.9129, 616.6115, 549…Descriptive statistics
Unique (#) Missing (%) Mean SD Min Median Max
1 Tax 31 0 20.2 4.5 7.5 20.0 29.0
2 Dlic 51 0 903.7 72.9 700.2 909.1 1075.3
3 Income 51 0 28.4 4.5 21.0 27.9 40.6
4 Miles 51 0 77418.6 52983.4 1534.0 78914.0 300767.0
5 Fuel 51 0 613.1 89.0 317.5 626.0 842.8Data visualization
Regression
Parameter | Coefficient | SE | 95% CI | t(46) | p
------------------------------------------------------------------------
(Intercept) | 383.96 | 165.75 | [ 50.32, 717.60] | 2.32 | 0.025
Tax | -4.11 | 2.11 | [ -8.36, 0.13] | -1.95 | 0.057
Dlic | 0.54 | 0.14 | [ 0.26, 0.81] | 3.90 | < .001
Income | -7.14 | 2.21 | [-11.58, -2.70] | -3.24 | 0.002
Miles | 4.02e-04 | 1.87e-04 | [ 0.00, 0.00] | 2.14 | 0.037 # Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-------------------------------------------------------
580.602 | 592.193 | 0.476 | 0.430 | 63.790 | 67.167Testing linearity (1/3)
Testing linearity (2/3)
Testing linearity (3/3)
Test stat Pr(>|Test stat|)
Tax -1.1363 0.26183
Dlic -2.4859 0.01670 *
Income 0.0500 0.96036
Miles -0.2036 0.83961
Tukey test -2.3136 0.02069 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Re-fitting regressions
Parameter | Coefficient | SE | 95% CI | t(46) | p
-----------------------------------------------------------------------
(Intercept) | 154.19 | 194.91 | [-238.13, 546.52] | 0.79 | 0.433
Tax | -4.23 | 2.03 | [ -8.31, -0.14] | -2.08 | 0.043
Dlic | 0.47 | 0.13 | [ 0.21, 0.73] | 3.67 | < .001
Income | -6.14 | 2.19 | [ -10.55, -1.72] | -2.80 | 0.008
Miles [log] | 26.76 | 9.34 | [ 7.96, 45.55] | 2.87 | 0.006 # Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-------------------------------------------------------
577.086 | 588.677 | 0.510 | 0.468 | 61.628 | 64.891Checking linearity (1/2)
Checking linearity (2/2)
Test stat Pr(>|Test stat|)
Tax -1.0767 0.28737
Dlic -1.9219 0.06096 .
Income -0.0840 0.93345
log(Miles) -1.3473 0.18463
Tukey test -1.4460 0.14818
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Interpreting the results
=============================================================
Model 1 Model 2
-------------------------------------------------------------
(Intercept) 383.9594 (165.7522) * 154.1928 (194.9062)
Tax -4.1145 (2.1073) -4.2280 (2.0301) *
Dlic 0.5353 (0.1373) *** 0.4719 (0.1285) ***
Income -7.1375 (2.2054) ** -6.1353 (2.1936) **
Miles 0.0004 (0.0002) *
log(Miles) 26.7552 (9.3374) **
-------------------------------------------------------------
R^2 0.4755 0.5105
Adj. R^2 0.4299 0.4679
Num. obs. 51 51
Num. df 46 46
F statistic 10.4272 *** 11.9924 ***
=============================================================
*** p < 0.001; ** p < 0.01; * p < 0.05
Model 1 Fuel ~ Tax + Dlic + Income + Miles
Model 2 Fuel ~ Tax + Dlic + Income + log(Miles)Application Exercise
ae04-02-MLR-linearity.Rmd
Takeaways
Linearity assumption
Diagnostics of the linearity
Linear transformations
References
