Heteroscedasticity

MP223 - Applied Econometrics Methods for the Social Sciences

Eduard Bukin

R setup

library(tidyverse)       # for data wrangling
library(alr4)            # for the data sets #
library(GGally)
library(ggpmisc)
library(parameters)
library(performance)
library(see)
library(car)
library(broom)
library(modelsummary)
library(texreg)
library(report)
library(wooldridge)

ggplot2::theme_set(ggplot2::theme_bw())

knitr::opts_chunk$set(
  fig.width = 12,
  fig.asp = 0.618,
  fig.retina = 3,
  dpi = 300,
  out.width = "100%", 
  message = FALSE,
  echo = TRUE, 
  cache = TRUE
)

arrange_diagnostics <-
    function(fit_obj_list,
             ...,
             which = c(1, 3),
             cols = NULL) {
        
        if (class(fit_obj_list) == "lm") fit_obj_list <- list(fit_obj_list)
        
        if (length(rlang::dots_list(...)) > 0)  fit_obj_list <- fit_obj_list %>% append(rlang::dots_list(...))
        
        if (is.null(cols)) cols = ceiling(length(fit_obj_list) * length(which) / 2)
        
        rows = ceiling(length(fit_obj_list) * length(which) / cols)
        
        if (length(which) > 1) {
            par(mfcol = c(rows, cols))
        } else {
            par(mfrow = c(rows, cols))
        }
        
        fit_obj_list %>%
            walk(~ {
                fitt <- .x
                which %>%
                    walk(~ {
                        plot(fitt, which = .x, main = as.character(fitt$call)[2])
                    })
            })
        par(mfrow = c(1, 1))
    }


my_gof <- function(fit_obj, digits = 4) {
    sum_fit <- summary(fit_obj)
    
    stars <- 
        pf(sum_fit$fstatistic[1],
           sum_fit$fstatistic[2], 
           sum_fit$fstatistic[3],
           lower.tail=FALSE) %>% 
        symnum(corr = FALSE, na = FALSE, 
               cutpoints = c(0,  .001,.01,.05,  1),
               symbols   =  c("***","**","*"," ")) %>% 
        as.character()
    
    list(
        # `R^2` = sum_fit$r.squared %>% round(digits),
        # `Adj. R^2` = sum_fit$adj.r.squared %>% round(digits),
        # `Num. obs.` = sum_fit$residuals %>% length(),
        `Num. df` = sum_fit$df[[2]],
        `F statistic` = str_c(sum_fit$fstatistic[1] %>% round(digits), " ", stars)
    )
}


screen_many_regs <-
    function(fit_obj_list, ..., digits = 4, single.row = TRUE) {
        
        if (class(fit_obj_list) == "lm") fit_obj_list <- list(fit_obj_list)
        
        if (length(rlang::dots_list(...)) > 0)  fit_obj_list <- fit_obj_list %>% append(rlang::dots_list(...))
        
        # browser()
        fit_obj_list %>%
            texreg::screenreg(
                custom.note =
                    list(., seq_along(.), names(.)) %>% 
                    pmap_chr(~ {
                        # browser()
                        # mod_nm <- str_c("Model ", ..2)
                        if (!is.null(..3) && ..3 != "") mod_nm <- ..3 else {
                            mod_nm <- str_c("Model ", ..2)
                        }
                        str_c(mod_nm, " ", as.character(..1$call)[[2]])
                    }) %>%
                    c("*** p < 0.001; ** p < 0.01; * p < 0.05", .) %>%
                    str_c(collapse = "\n") ,
                digits = digits,
                single.row = single.row,
                custom.gof.rows =
                    map(., ~my_gof(.x, digits)) %>%
                    transpose() %>%
                    map(unlist),
                reorder.gof = c(3, 4, 5, 1, 2)
            )
    }

Assumption 5. Error Terms Homoscedasticity

\[Var(u|x_{i1}, x_{i2}, \cdots , x_{ik}) = \sigma^2\]

Causes of heteroscedasticity

  • Functional relationship is misspecified;

  • Omitting an important factor;

  • Nature of data generation process;

Consequence:

  • Estimates may not be biased, but;

  • Standard errors are inefficient;

  • Hypothesis testing on the coefficients may be False because under heteroskedasticity our estimates are inefficient;

Detection

  • graphical: residuals vs regressors and fitted values plots;

  • Formal statistical testing:

    • Breusch-Pagan heteroskedasticiy test;

    • White test;

    • Goldfeld-Quandt heteroskedasticity test;

Solutions:

  • Re specify the model;

  • Choose different regressors;

    • attempt to correct SE with alternative estimation procedures - use the heteroskedasticity-consistent (robust) standard errors!

  • See also: “Assumption AMLR.5” in (Wooldridge 2020) ;

AMLR. 5. Heteroscedasticity examples (1/2)

AMLR. 5. Heteroscedasticity examples (2/2)

Example 1. Heteroscedasticity in the wage equation

Data

Code 
woolwage2 <-
  wooldridge::wage2 %>%
  as_tibble %>%
  select(wage, educ, tenure, abil = KWW)
glimpse(woolwage2)
Rows: 935
Columns: 4
$ wage   <int> 769, 808, 825, 650, 562, 1400, 600, 1081, 1154, 1000, 930, 921,…
$ educ   <int> 12, 18, 14, 12, 11, 16, 10, 18, 15, 12, 18, 14, 15, 16, 16, 10,…
$ tenure <int> 2, 16, 9, 7, 5, 2, 0, 14, 1, 16, 13, 11, 3, 2, 9, 2, 9, 10, 7, …
$ abil   <int> 35, 41, 46, 32, 27, 43, 24, 50, 37, 44, 44, 45, 40, 24, 47, 37,…
Code 
report(woolwage2) %>% as_tibble()
# A tibble: 4 × 11
  Variable n_Obs   Mean     SD Median    MAD   Min   Max Skewness Kurtosis
  <chr>    <int>  <dbl>  <dbl>  <int>  <dbl> <int> <int>    <dbl>    <dbl>
1 wage       935 958.   404.      905 369.     115  3078    1.20     2.72 
2 educ       935  13.5    2.20     12   1.48     9    18    0.549   -0.735
3 tenure     935   7.23   5.08      7   5.93     0    22    0.433   -0.799
4 abil       935  35.7    7.64     37   7.41    12    56   -0.293   -0.317
# … with 1 more variable: percentage_Missing <dbl>

The model

Code 
fit_1 <- lm(wage ~ educ + abil, data = woolwage2)
screen_many_regs(fit_1, single.row = F)

=========================
             Model 1     
-------------------------
(Intercept)  -71.0911    
             (81.5735)   
educ          43.4601 ***
              (6.0189)   
abil          12.4130 ***
              (1.7308)   
-------------------------
R^2            0.1537    
Adj. R^2       0.1519    
Num. obs.    935         
Num. df      932         
F statistic   84.6348 ***
=========================
*** p < 0.001; ** p < 0.01; * p < 0.05

Visual diagnostics:

library(performance)
check_model(fit_1, check = "linearity") %>% plot()

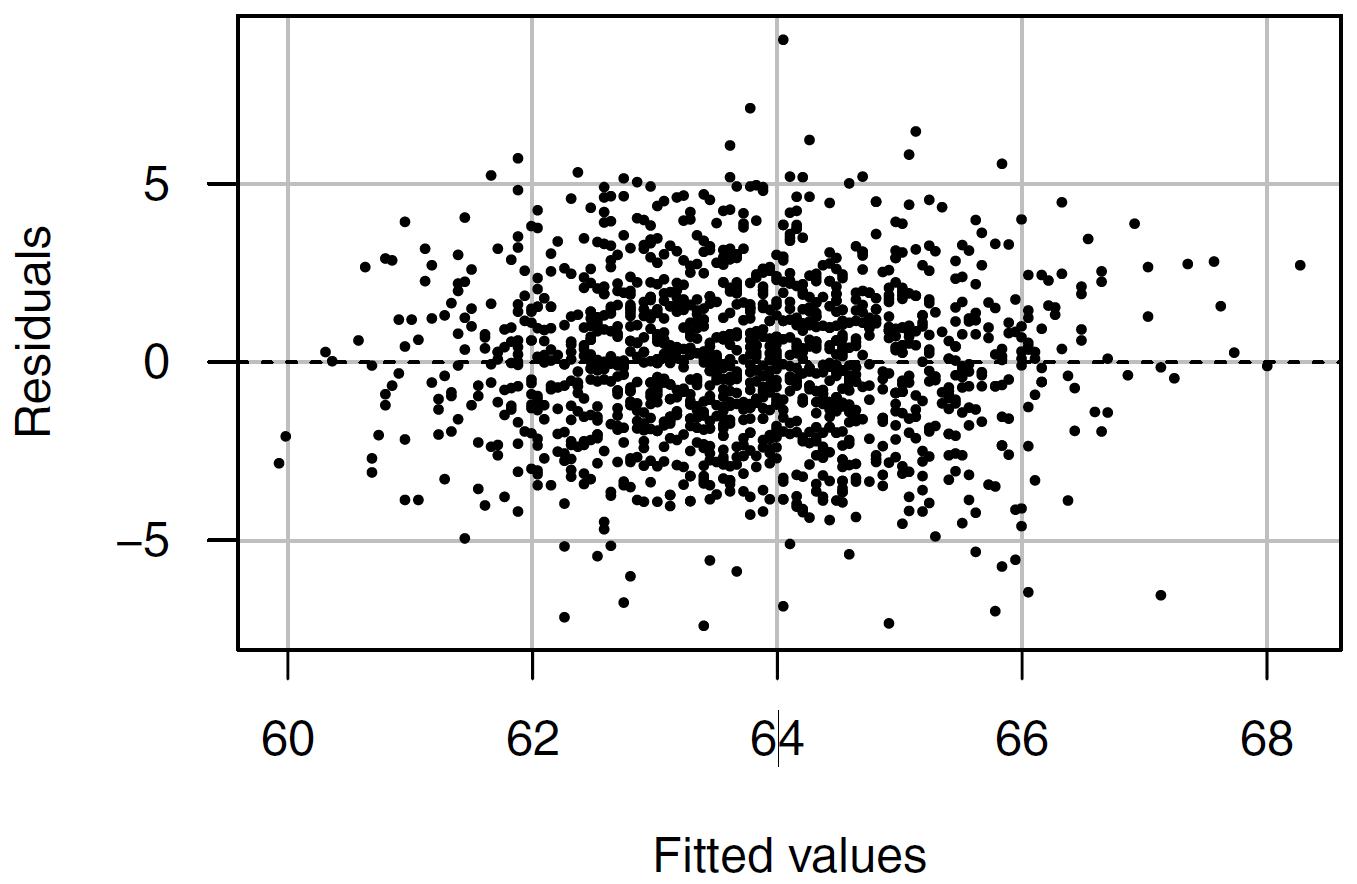
Residuals vs Fitted

Residuals vs Fitted

Residuals vs Fitted

Standardized residuals vs Fitted

(sqrt) Standardized residuals vs Fitted

(sqrt) Standardized residuals vs Fitted

Residuals vs Fitted + (sqrt) Standardized residuals

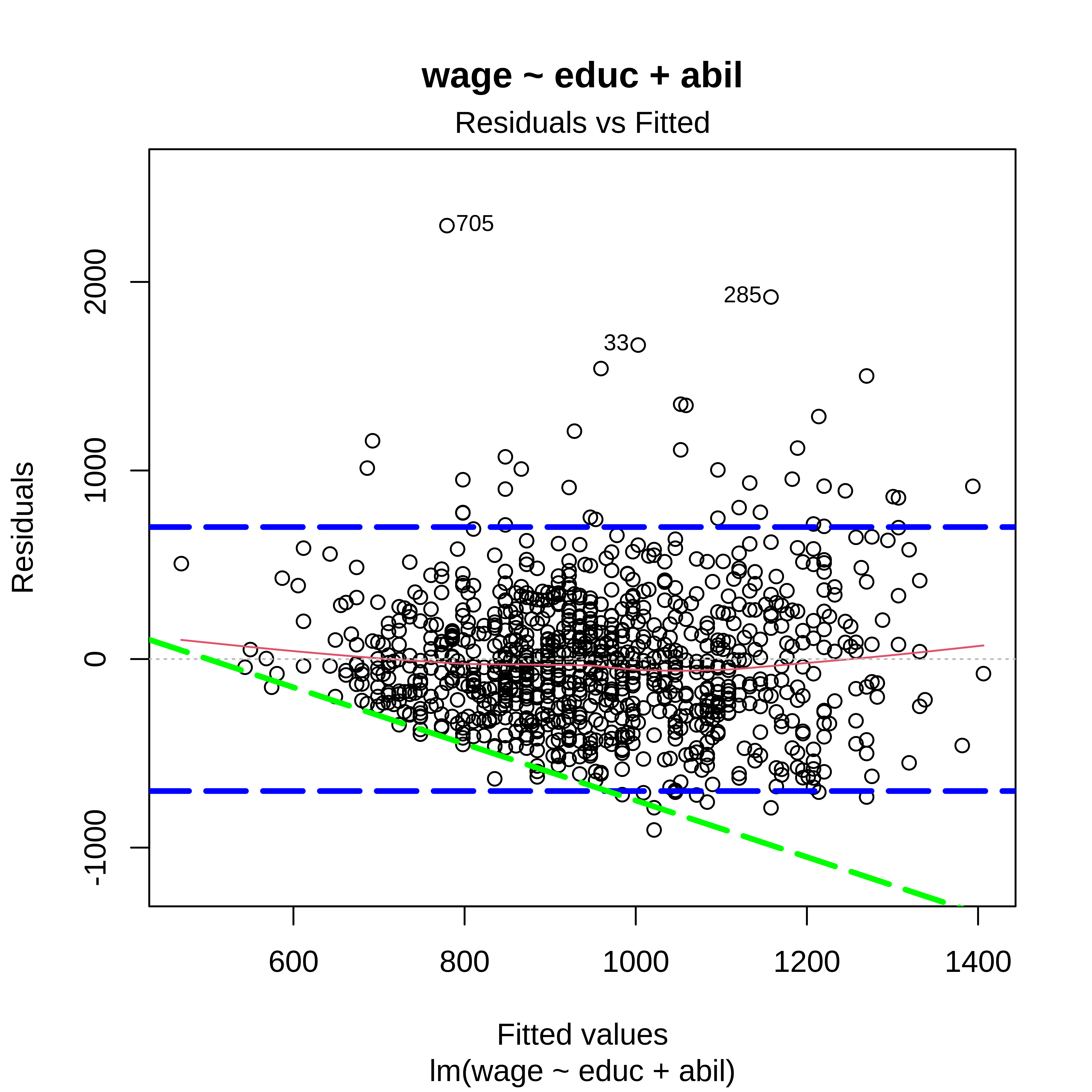
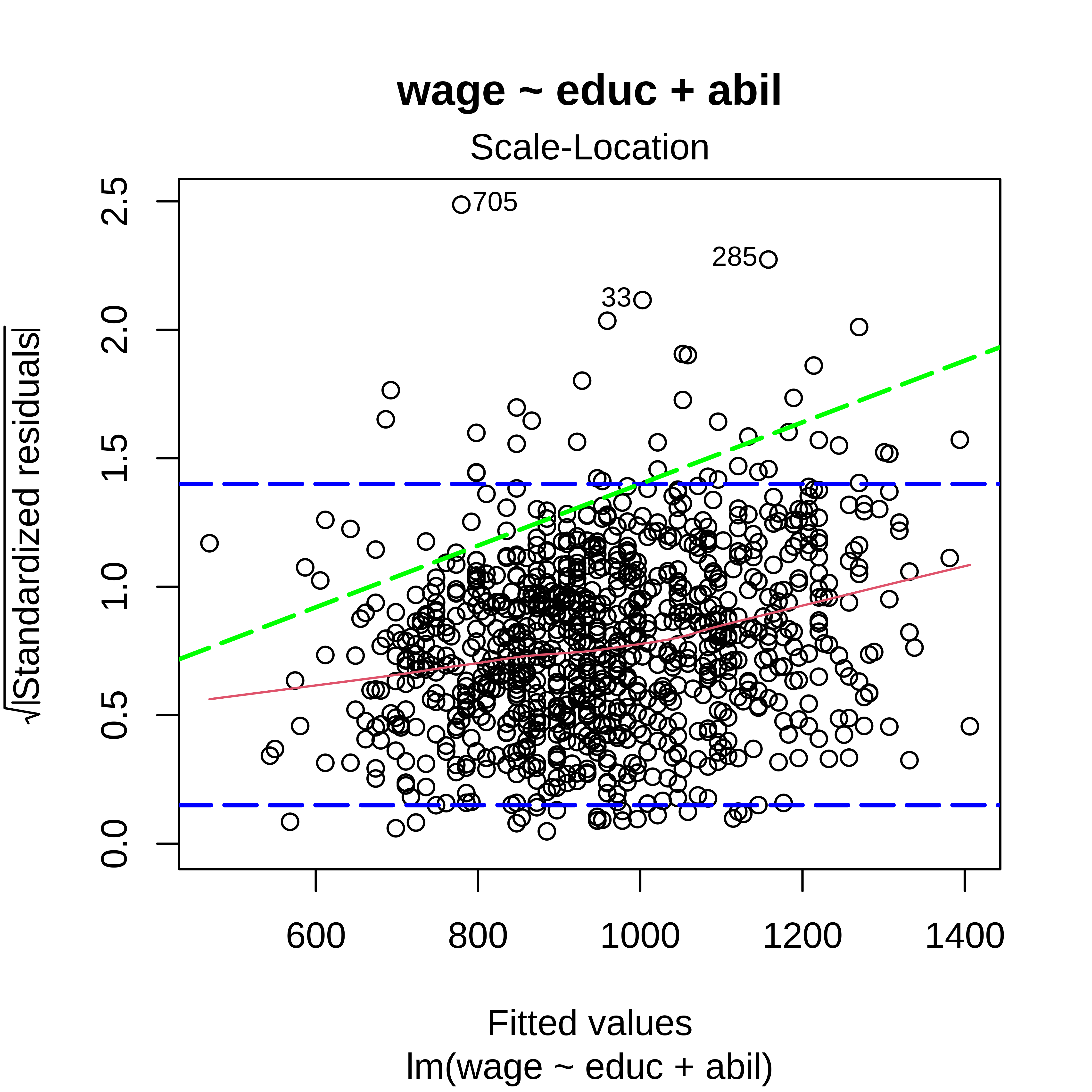
Residuals vs Fitted + (sqrt) Standardized residuals

check_model(fit_1, check = c("linearity", "homogeneity")) %>% plot()

Statistical tests

library(performance)
check_heteroscedasticity(fit_1)
Warning: Heteroscedasticity (non-constant error variance) detected (p < .001).

  • \(H_0\) error terms are homoscedastic.

  • \(H_1\) we have heteroscedastic error terms.

  • We reject \(H_0\) if p-value < 0.05 (at 5% significance level).

The Breusch-Pagan test

library(lmtest)
bptest(fit_1)

    studentized Breusch-Pagan test

data:  fit_1
BP = 18.002, df = 2, p-value = 0.0001233
library(car)
ncvTest(fit_1)
Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 46.71456, Df = 1, p = 8.2117e-12

White test: a special case of the BP test

bptest(fit_1, ~ educ * abil + educ + I(educ^2) + I(abil^2), 
       data = woolwage2)

    studentized Breusch-Pagan test

data:  fit_1
BP = 25.85, df = 5, p-value = 9.541e-05

Goldfeld-Quandt test: Stable with non-normal data

# ?bptest ## install.packages("lmtest") is is not installed
gqtest(fit_1)

    Goldfeld-Quandt test

data:  fit_1
GQ = 0.96373, df1 = 465, df2 = 464, p-value = 0.6547
alternative hypothesis: variance increases from segment 1 to 2
gqtest(fit_1, 0.15)

    Goldfeld-Quandt test

data:  fit_1
GQ = 1.1162, df1 = 792, df2 = 137, p-value = 0.2125
alternative hypothesis: variance increases from segment 1 to 2

Conclusions on Heteroskedasticity in the wage equation

  • We have:

    • Heteroskedasticity;

    • Inappropriate model specification;

    • Possible linearity assumption violation;

  • Solutions:

    • Model re-specification;

    • Correcting standard errors;

Model adjustment:

Code 
fit_1 <- lm(wage ~ educ + abil, data = woolwage2)
fit_2 <- lm(log(wage) ~ educ + abil , data = woolwage2)
fit_3 <- lm(log(wage) ~ educ + abil + tenure , data = woolwage2)
screen_many_regs(fit_1, fit_2, fit_3, single.row = T)

=================================================================================
             Model 1                 Model 2                Model 3              
---------------------------------------------------------------------------------
(Intercept)  -71.0911 (81.5735)        5.7620 (0.0858) ***    5.6751 (0.0859) ***
educ          43.4601  (6.0189) ***    0.0436 (0.0063) ***    0.0471 (0.0063) ***
abil          12.4130  (1.7308) ***    0.0120 (0.0018) ***    0.0103 (0.0018) ***
tenure                                                        0.0140 (0.0025) ***
---------------------------------------------------------------------------------
R^2            0.1537                  0.1378                 0.1652             
Adj. R^2       0.1519                  0.1359                 0.1625             
Num. obs.    935                     935                    935                  
Num. df      932                     932                    931                  
F statistic   84.6348 ***             74.4578 ***            61.4301 ***         
=================================================================================
*** p < 0.001; ** p < 0.01; * p < 0.05
Model 1 wage ~ educ + abil
Model 2 log(wage) ~ educ + abil
Model 3 log(wage) ~ educ + abil + tenure

Linearity + Heteroskedasticity (1/2)

Linearity + Heteroskedasticity (2/2)

Heteroskedasticity

bptest(fit_2, data = woolwage2)

    studentized Breusch-Pagan test

data:  fit_2
BP = 2.7321, df = 2, p-value = 0.2551
bptest(fit_2, ~ educ * abil + I(educ^2) + I(abil^2), data = woolwage2)

    studentized Breusch-Pagan test

data:  fit_2
BP = 10.29, df = 5, p-value = 0.06741
bptest(fit_3, data = woolwage2)

    studentized Breusch-Pagan test

data:  fit_3
BP = 36.301, df = 3, p-value = 6.466e-08
bptest(fit_3, ~ educ * abil + educ * tenure + abil * tenure +
      I(educ^2) + I(abil^2) + I(tenure^2), data = woolwage2)

    studentized Breusch-Pagan test

data:  fit_3
BP = 60.481, df = 9, p-value = 1.083e-09

Conclusions:

parameters(fit_3)
Parameter   | Coefficient |       SE |       95% CI | t(931) |      p
---------------------------------------------------------------------
(Intercept) |        5.68 |     0.09 | [5.51, 5.84] |  66.09 | < .001
educ        |        0.05 | 6.26e-03 | [0.03, 0.06] |   7.52 | < .001
abil        |        0.01 | 1.82e-03 | [0.01, 0.01] |   5.68 | < .001
tenure      |        0.01 | 2.52e-03 | [0.01, 0.02] |   5.54 | < .001

Model fit_3 describes the data in the best way because:

  • Reduces omitted variable bias;
  • Resolves non-linearity;
  • But it still suffers from the heteroskedasticity!!

Robust standard errors

Robust estimators for variance covariance matrix:

  • sandwich::vcovHC - heteroskedasticity consistent

  • sandwich::vcovCL - clustered SE

  • clubSandwich::vcovCR - clustered heteroskedasticity consistent SE

  • sandwich::vcovHAC - heteroskedasticity and autocorrelation consistent

  • Estimation methods:

    • HC3 - optimal one as per Long & Ervin (2000)
    • HC1 - default in Stata

Robust standard errors (1)

Old estimates:

Code 
coeftest(fit_3)

t test of coefficients:

             Estimate Std. Error t value  Pr(>|t|)    
(Intercept) 5.6750741  0.0858710 66.0884 < 2.2e-16 ***
educ        0.0470780  0.0062604  7.5199 1.288e-13 ***
abil        0.0103191  0.0018174  5.6781 1.820e-08 ***
tenure      0.0139630  0.0025226  5.5352 4.042e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Robust standard errors (1)

Robust estimates:

Code 
library(car)
library(lmtest)
library(sandwich)
coeftest(fit_3, vcov. = sandwich::vcovHC(fit_3, type = "HC3"))

t test of coefficients:

             Estimate Std. Error t value  Pr(>|t|)    
(Intercept) 5.6750741  0.0848077 66.9169 < 2.2e-16 ***
educ        0.0470780  0.0067209  7.0047 4.740e-12 ***
abil        0.0103191  0.0019766  5.2205 2.201e-07 ***
tenure      0.0139630  0.0026470  5.2751 1.651e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Robust standard errors (2)

coeftest(fit_3, vcov = vcovHC(fit_3, type = "HC3"))    

t test of coefficients:

             Estimate Std. Error t value  Pr(>|t|)    
(Intercept) 5.6750741  0.0848077 66.9169 < 2.2e-16 ***
educ        0.0470780  0.0067209  7.0047 4.740e-12 ***
abil        0.0103191  0.0019766  5.2205 2.201e-07 ***
tenure      0.0139630  0.0026470  5.2751 1.651e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
coeftest(fit_3, vcov = vcovHC(fit_3, type = "HC1"))    

t test of coefficients:

             Estimate Std. Error t value  Pr(>|t|)    
(Intercept) 5.6750741  0.0845112 67.1517 < 2.2e-16 ***
educ        0.0470780  0.0066968  7.0299 3.994e-12 ***
abil        0.0103191  0.0019690  5.2407 1.979e-07 ***
tenure      0.0139630  0.0026387  5.2917 1.512e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Robust standard errors (3)

Comparing Robust standard errors


=============================================================================
             fit_2 - Regular  fit_2 - Robust  fit_3 - Regular  fit_3 - Robust
-----------------------------------------------------------------------------
(Intercept)    5.76198 ***      5.76198 ***     5.67507 ***      5.67507 *** 
              (0.08576)        (0.08332)       (0.08587)        (0.08481)    
educ           0.04362 ***      0.04362 ***     0.04708 ***      0.04708 *** 
              (0.00633)        (0.00668)       (0.00626)        (0.00672)    
abil           0.01202 ***      0.01202 ***     0.01032 ***      0.01032 *** 
              (0.00182)        (0.00193)       (0.00182)        (0.00198)    
tenure                                          0.01396 ***      0.01396 *** 
                                               (0.00252)        (0.00265)    
-----------------------------------------------------------------------------
R^2            0.13777          0.13777         0.16524          0.16524     
Adj. R^2       0.13592          0.13592         0.16255          0.16255     
Num. obs.    935              935             935              935           
=============================================================================
*** p < 0.001; ** p < 0.01; * p < 0.05

Interpretation

fit_3

Call:
lm(formula = log(wage) ~ educ + abil + tenure, data = woolwage2)

Coefficients:
(Intercept)         educ         abil       tenure  
    5.67507      0.04708      0.01032      0.01396  
model_parameters(fit_3, vcov = "HC3")
Parameter   | Coefficient |       SE |       95% CI | t(931) |      p
---------------------------------------------------------------------
(Intercept) |        5.68 |     0.08 | [5.51, 5.84] |  66.92 | < .001
educ        |        0.05 | 6.72e-03 | [0.03, 0.06] |   7.00 | < .001
abil        |        0.01 | 1.98e-03 | [0.01, 0.01] |   5.22 | < .001
tenure      |        0.01 | 2.65e-03 | [0.01, 0.02] |   5.28 | < .001
model_performance(fit_3)
# Indices of model performance

AIC       |       BIC |    R2 | R2 (adj.) |  RMSE | Sigma
---------------------------------------------------------
13553.141 | 26254.081 | 0.165 |     0.163 | 0.385 | 0.385

References

https://ebukin.github.io/mp223-2022-aem-R-public/

Wooldridge, M. Jeffrey. 2020. Introductory Econometrics: A Modern Approach. South-Western. https://www.cengage.uk/shop/isbn/9781337558860.