Simple regression

MP223 - Applied Econometrics Methods for the Social Sciences

Eduard Bukin

R setup

# load packages
library(tidyverse)       # for data wrangling
library(alr4)            # for the data sets #
# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_bw())
# set default figure parameters for knitr
knitr::opts_chunk$set(
  fig.width = 8,
  fig.asp = 0.618,
  fig.retina = 3,
  dpi = 300,
  out.width = "80%"
)

Data

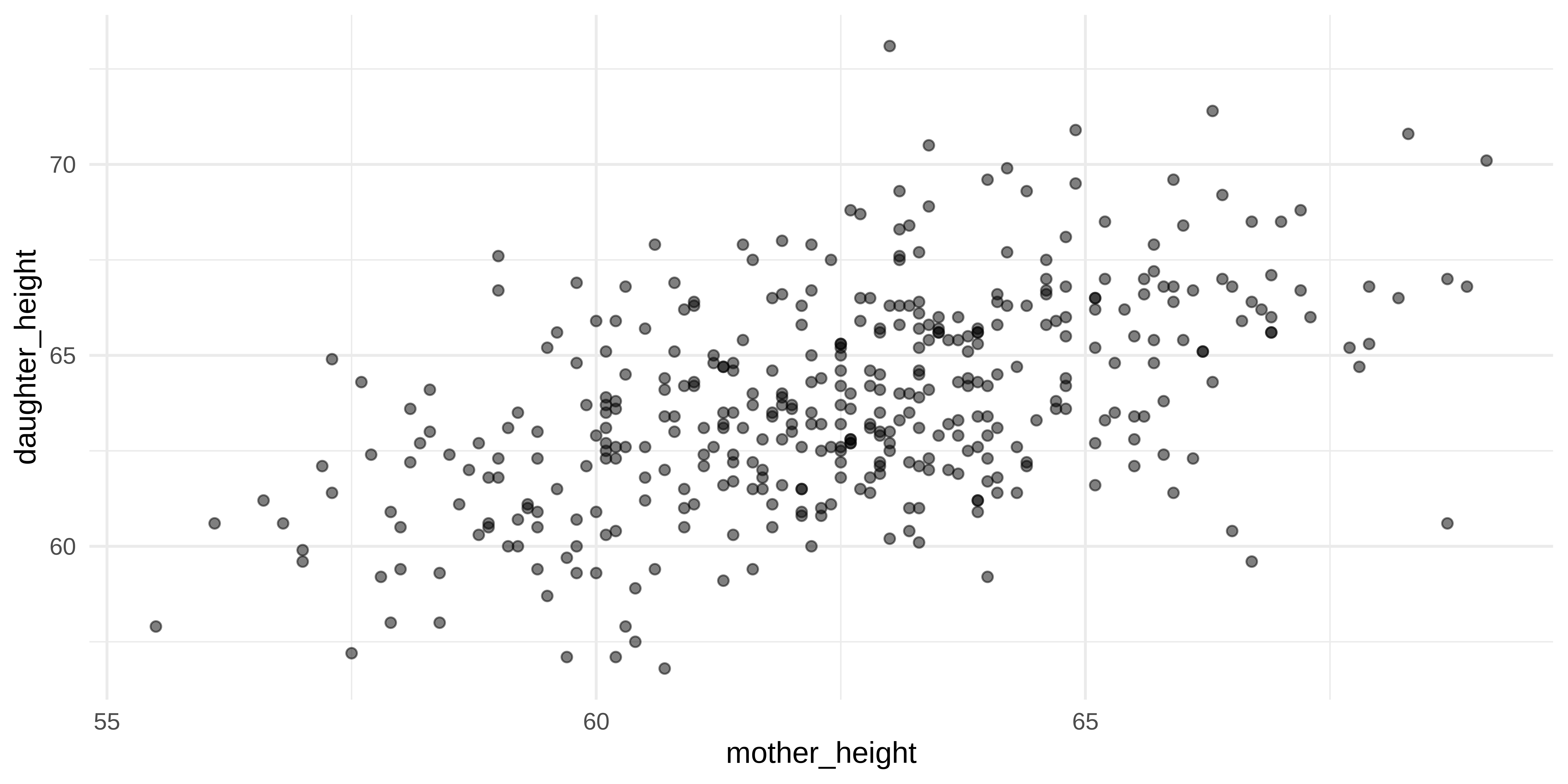
Pearson-Lee data

  • Data used is published in (Pearson and Lee 1903).

  • Karl Pearson collected data on over 1100 families in England in the period 1893 to 1898;

  • Heights of mothers mheight and daughters dheight was recorded for 1375 observations.

  • We rely on the examples of SLR in (Weisberg 2005)

Data loading and preparation

  • Loading data
  • Converting data frame into a tibble() object
  • Renaming variables
  • Glimpse of data
Code 
# Note, we use `sample_n(400)` to randomly select only 400 observations
dta <- 
  alr4::Heights %>% 
  as_tibble() %>% 
  rename(mother_height = mheight,
         daughter_height = dheight) %>% 
  sample_n(400)
glimpse(dta)
Rows: 400
Columns: 2
$ mother_height   <dbl> 58.8, 65.4, 65.5, 63.2, 60.1, 61.2, 60.8, 63.7, 63.8, …
$ daughter_height <dbl> 62.7, 66.2, 62.8, 62.2, 65.1, 64.8, 63.4, 64.3, 62.5, …

Exploring data (Scatter plot)

Code 
plt <- 
  dta %>% 
  ggplot() + 
  aes(x = mother_height, y = daughter_height) + 
  geom_point(alpha = 0.5) + 
  theme_minimal()
plt

  • What alpha = 0.5 stands for?
  • Add labels.
  • change color of points (add color = "red" after alpha separating arguments with comma)
Code 
dta %>% 
  ggplot() + 
  aes(x = mother_height, y = daughter_height) + 
  geom_point(alpha = 0.5) + 
  labs(x = "___________", 
       y = "___________")

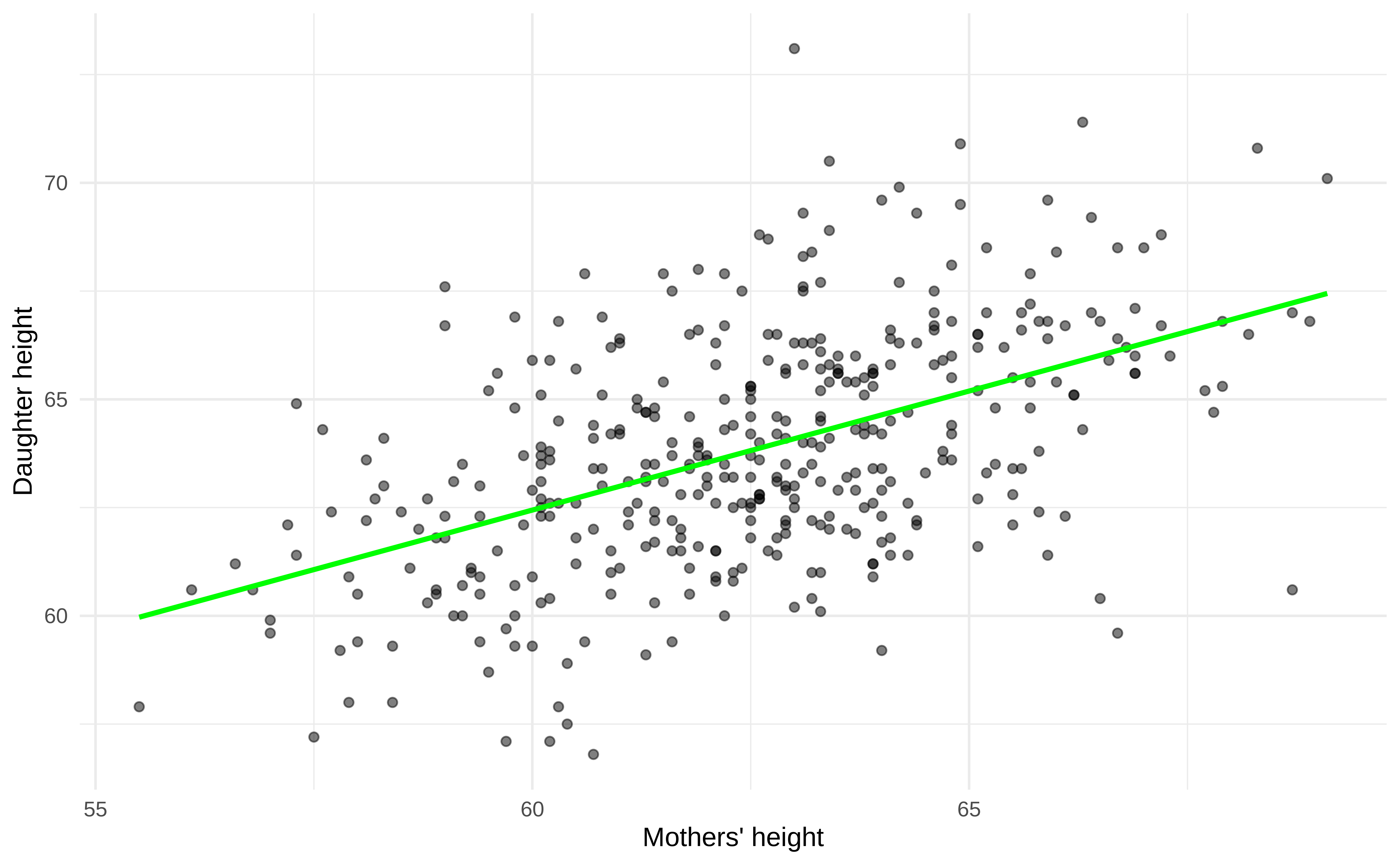
Simple Linear Regression

Simple regression line

\(Y \\ = \color{green}{f(X)} \\ + \text{Error term} \\ = \color{green}{E[Y|X]} + \epsilon\)

Code 
fit <- 
  lm(daughter_height ~ mother_height, data = dta)
plt <- 
  plt + 
  labs(x = "Mothers' height", 
       y = "Daughter height") + 
  geom_smooth(method = "lm", 
              color = "green", 
              se = FALSE) + 
  theme_minimal()
plt

Simple regression

\[\Large{Y = \beta_0 + \beta_1 X}\]

  • \(Y\): dependent variable, observed values
  • \(X\): independent variable
  • \(\beta_1\): True slope
  • \(\beta_0\): True intercept
  • Note, in the population regression function, there is no error terms!

Estimated simple regression

\[\Large{\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1 X}\]

  • \(\hat{Y}\): fitted values, predicted values
  • \(\hat{\beta}_1\): Estimated slope
  • \(\hat{\beta}_0\): Estimated intercept
  • No error term!

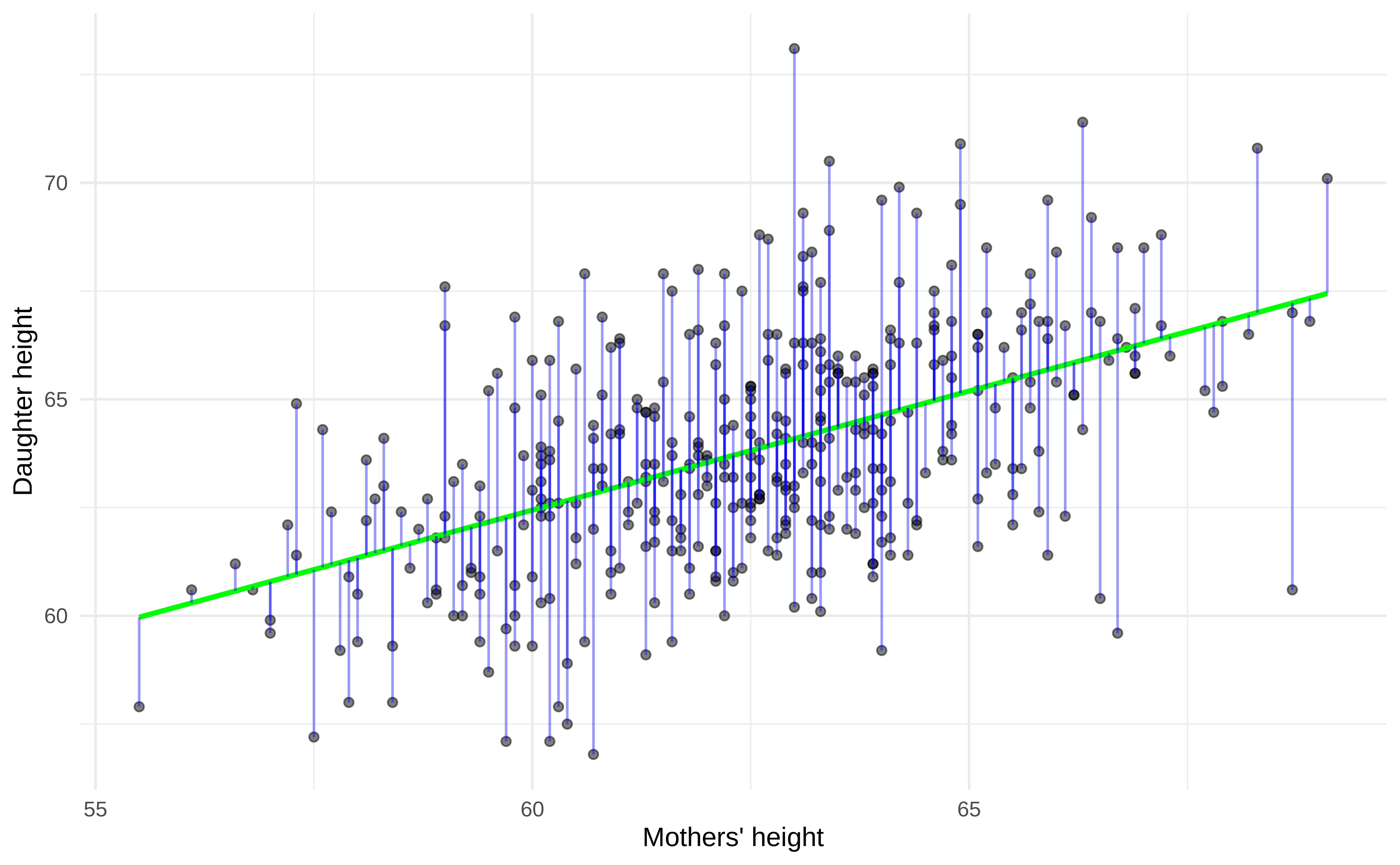
Residuals

\(Y \\ = \color{green}{f(X)} \\ + \color{blue}{\text{Error term}} \\ = \color{green}{E[Y|X]} + \color{blue}{\epsilon}\)

Code 
plt + 
  geom_segment(
    aes(x = mother_height, xend = mother_height,
        y = daughter_height, yend = predict(fit)), 
    color = "blue",
    alpha = 0.4
  )

Residuals

  • \(\text{residuals} \\ = \text{observed} - \text{predicted} \\ = \epsilon = Y - \hat{Y}\)

  • \({Y = \hat{\beta}_0 + \hat{\beta}_1 X + \epsilon}\)

  • \(\epsilon\) is the error term or residual

  • For each specific observation \(i\)

  • residual \(e_i = y_i - \hat{y_i}\)

  • squared residual \(e_i^2 = (y_i - \hat{y_i})^2\)

Ordinary Least Square (OLS)

Ordinary Least Square (OLS)

  • “finds” values for \(\hat{\beta}_0\) and \(\hat{\beta}_1\)

  • each new value of \(\hat{\beta}_0\) and \(\hat{\beta}_1\) generates new regression line;

Code 
plt + 
  geom_segment(
    aes(x = mother_height, xend = mother_height,
        y = daughter_height, yend = predict(fit)), 
    color = "blue",
    alpha = 0.4
  ) + 
  geom_abline(intercept = 33, slope = 0.49, color = "black") + 
  geom_abline(intercept = 5, slope = 0.95, color = "black") + 
  geom_abline(intercept = 25, slope = 0.62, color = "black")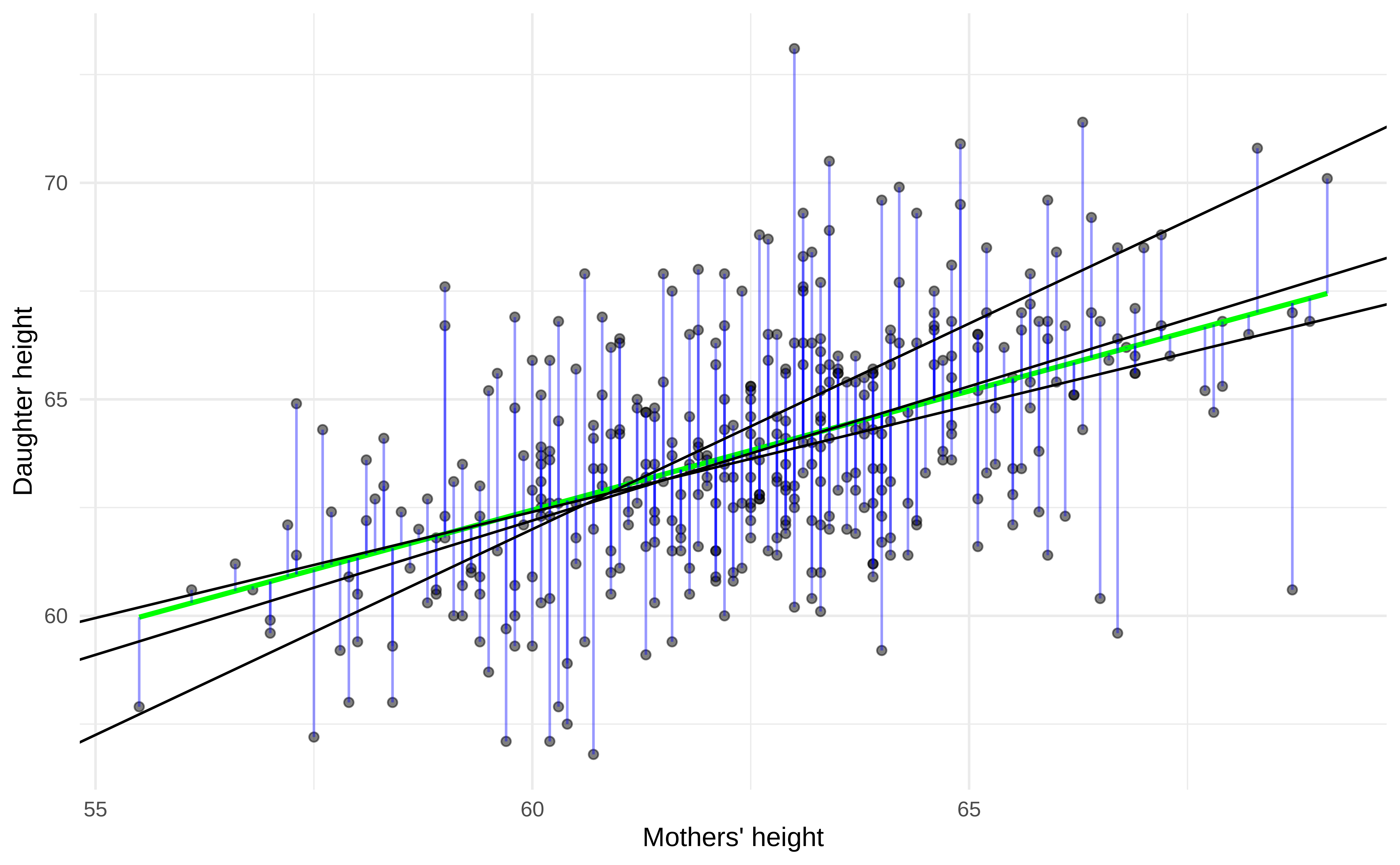

Ordinary Least Square (OLS)

the OLS finds such values of \(\hat{\beta}_0\) and \(\hat{\beta}_1\) that minimizes the sum of squared residuals:

\[ \Large{ SSR = \sum_{i}^{n}{e_i^2} = \sum_{i}^{n}{(y_i - \hat{y_i})^2} \\ = {[e_1^2 + e_2^2 + ... + e_n^2]} } \]

Properties of OLS

  • The regression line goes through the center of all point.

  • The sum of the residuals (not squared) is zero: \(\sum_{i}^n e_i = 0\)

  • Zero correlation between residuals and regressors \(Cov(X,\epsilon) = 0\)

  • Predicted value of \(Y\), when all regressors are at means \(\bar{X}\) is the mean of \(\bar{Y}\): \(E[Y|\bar{X}] = \bar{Y}\)

Interpretation

Regression coefficients

fit <- lm(daughter_height ~ mother_height, data = dta)
fit

Call:
lm(formula = daughter_height ~ mother_height, data = dta)

Coefficients:
  (Intercept)  mother_height  
      29.4551         0.5498

Regression summary (1/3)

summary(fit)

Call:
lm(formula = daughter_height ~ mother_height, data = dta)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.6255 -1.5767 -0.0878  1.3916  9.0083 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)   29.45511    2.91727   10.10   <2e-16 ***
mother_height  0.54979    0.04662   11.79   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.337 on 398 degrees of freedom
Multiple R-squared:  0.2589,    Adjusted R-squared:  0.2571 
F-statistic: 139.1 on 1 and 398 DF,  p-value: < 2.2e-16

Regression summary (2/3)

library(broom)
tidy(fit)
# A tibble: 2 × 5
  term          estimate std.error statistic  p.value
  <chr>            <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)     29.5      2.92        10.1 1.71e-21
2 mother_height    0.550    0.0466      11.8 9.88e-28
glance(fit)
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.259         0.257  2.34      139. 9.88e-28     1  -906. 1818. 1830.
# … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

Regression summary (3/3)

library(parameters)
parameters(fit)
Parameter     | Coefficient |   SE |         95% CI | t(398) |      p
---------------------------------------------------------------------
(Intercept)   |       29.46 | 2.92 | [23.72, 35.19] |  10.10 | < .001
mother height |        0.55 | 0.05 | [ 0.46,  0.64] |  11.79 | < .001
library(performance)
performance(fit)
# Indices of model performance

AIC      |      BIC |    R2 | R2 (adj.) |  RMSE | Sigma
-------------------------------------------------------
1818.301 | 1830.276 | 0.259 |     0.257 | 2.331 | 2.337

Intercept

  • Important in the context of the data.

  • Value of \(Y\) when all \(X\) are zero.

Slope

Marginal effect or unit change in \(Y\) on average, when \(X\) is being change by on unit, keeping all other regressors fixed.

  • When mother’s height increases by 1 inch, the height of a daughter increases by \(\hat{\beta_1}\) inches, keeping other variables constant.

Residuals and Fitted values

Residuals

# With `[1:20]` we foce R only to print first 20 values
residuals(fit)[1:20]
         1          2          3          4          5          6          7 
 0.9173961  0.7887997 -2.6661790 -2.0016682  2.6026726  1.6979065  0.5178215 
         8          9         10         11         12         13         14 
-0.1765618 -2.0315406 -1.5917107 -5.4523061 -5.1774125  0.8022473 -1.4757112 
        15         16         17         18         19         20 
-3.4674550  4.0178215 -0.6813279 -3.6462641  1.8927151 -4.2860940 
resid(fit)[1:20]
         1          2          3          4          5          6          7 
 0.9173961  0.7887997 -2.6661790 -2.0016682  2.6026726  1.6979065  0.5178215 
         8          9         10         11         12         13         14 
-0.1765618 -2.0315406 -1.5917107 -5.4523061 -5.1774125  0.8022473 -1.4757112 
        15         16         17         18         19         20 
-3.4674550  4.0178215 -0.6813279 -3.6462641  1.8927151 -4.2860940

Fitted

# With `[1:20]` we foce R only to print first 20 values
fitted(fit)[1:20]
       1        2        3        4        5        6        7        8 
61.78260 65.41120 65.46618 64.20167 62.49733 63.10209 62.88218 64.47656 
       9       10       11       12       13       14       15       16 
64.53154 64.09171 62.55231 62.27741 61.39775 66.67571 62.16746 62.88218 
      17       18       19       20 
65.08133 65.24626 62.60728 65.68609

Residuals vs fitted (1/3)

dta_1 <- 
  dta %>% 
  mutate(fitted = fitted(fit)) %>% 
  mutate(residuals = resid(fit))

glimpse(dta_1)
Rows: 400
Columns: 4
$ mother_height   <dbl> 58.8, 65.4, 65.5, 63.2, 60.1, 61.2, 60.8, 63.7, 63.8, …
$ daughter_height <dbl> 62.7, 66.2, 62.8, 62.2, 65.1, 64.8, 63.4, 64.3, 62.5, …
$ fitted          <dbl> 61.78260, 65.41120, 65.46618, 64.20167, 62.49733, 63.1…
$ residuals       <dbl> 0.9173961, 0.7887997, -2.6661790, -2.0016682, 2.602672…

Residuals vs fitted (2/3)

dta_1 %>% 
  ggplot() + 
  aes(x = fitted, y = residuals) + 
  geom_point()

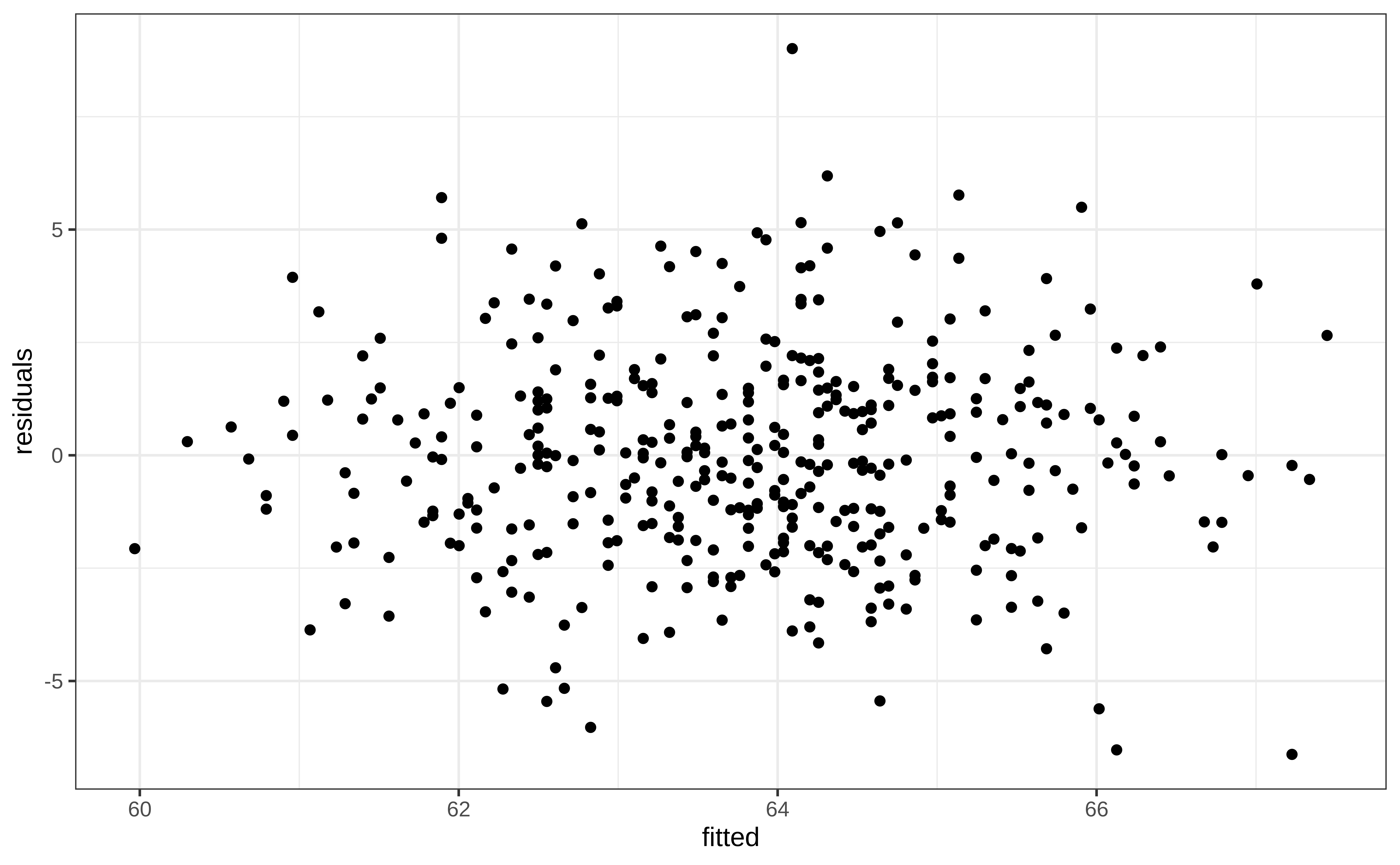
Residuals vs fitted (3/3)

library(performance)
library(see)
check_model(fit, check = "linearity", panel = FALSE)
$NCV

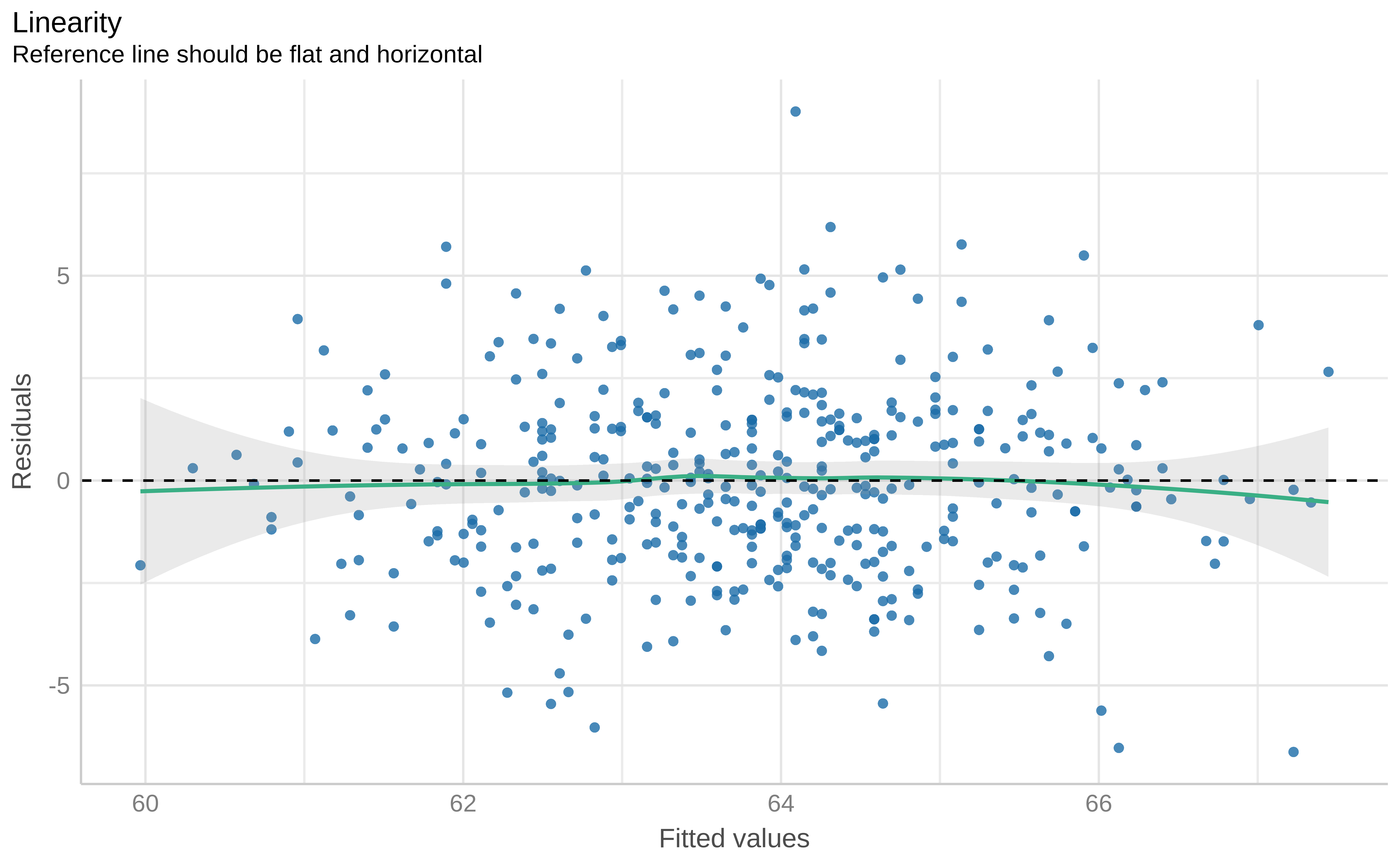
Takeaways

Takeaway

  • Simple linear regression
  • OLS
  • Slope and Intercept (interpretation)
  • Fitted values
  • Residuals
  • Residuals vs Fitted
  • fitting regression: fit()
  • regression summary: summary(), tidy(), glance(), parameters(), performance() , check_model() , fitted() , residuals() , resid()
  • packages: broom, parameters and performance

Homework

Create an R Script out of the R code in the presentation.

References

References

https://ebukin.github.io/mp223-2022-aem-R-public/

Pearson, Karl, and Alice Lee. 1903. “On the Laws of Inheritance in Man: I. Inheritance of Physical Characters.” Biometrika 2 (4): 357. https://doi.org/10.2307/2331507.
Weisberg, Sanford. 2005. Applied Linear Regression. John Wiley & Sons, Inc. https://doi.org/10.1002/0471704091.